Квазичастица — это объект, который описывается гармонической плоской волной 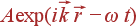 (это математическое определение).
(это математическое определение).
Каждая квазичастица обладает определенной энергией 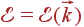 , а волна — соответствующей частотой,
, а волна — соответствующей частотой, 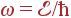 . Зависимость
. Зависимость 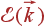 (или
(или 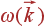 ), как уже говорилось, называется законом дисперсии, это самая важная характеристика квазичастицы. Иногда вместо зависимости
), как уже говорилось, называется законом дисперсии, это самая важная характеристика квазичастицы. Иногда вместо зависимости 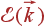 используют зависимость
используют зависимость  , где
, где 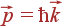 — импульс частицы. В простейший случаях энергия зависит только от модуля волнового вектора (свободные электроны, фотоны в вакууме), но в общем случае зависит и от направления (большинство квазичастиц в кристаллах).
— импульс частицы. В простейший случаях энергия зависит только от модуля волнового вектора (свободные электроны, фотоны в вакууме), но в общем случае зависит и от направления (большинство квазичастиц в кристаллах).
Обозначим через Δ N число разрешенных состояний квазичастицы для единичного нормировочного объема (V = 1), энергии которых находятся в интервале от 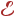 до
до  , где
, где  .
.
Плотностью состояний квазичастицы 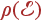 называется предел отношения
называется предел отношения 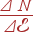 при
при 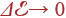 , т. е. число состояний на единицу объема, приходящихся на единичный интервал энергии.
, т. е. число состояний на единицу объема, приходящихся на единичный интервал энергии.
Сосчитаем Δ N. Проведем в k -пространстве две поверхности постоянной энергии, соответствующие энергиям 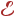 и
и  , где
, где  . Эти поверхности для двумерного случая изображены на рис. 3, где также нарисована двумерная решетка, в узлах которой располагаются разрешенные значения волновых векторов.
. Эти поверхности для двумерного случая изображены на рис. 3, где также нарисована двумерная решетка, в узлах которой располагаются разрешенные значения волновых векторов.
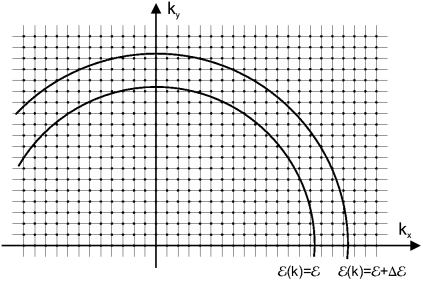 Рис. 3.
Рис. 3.
|
Число состояний Δ N с энергиями от 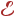 до
до  равно отношению объема Δ 3 k, заключенному между поверхностями, к объему δ k, приходящемуся на одно разрешенное состояние.
равно отношению объема Δ 3 k, заключенному между поверхностями, к объему δ k, приходящемуся на одно разрешенное состояние.
Если энергия квазичастицы 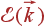 зависит только от модуля волнового вектора, то поверхности постоянной энергии в k -пространстве представляют собой сферы (в двумерном пространстве на картинке — круги). Объем тонкого шарового слоя толщиной Δ k равен 4 π k 2 Δ k. Учитывая, что δ k = (2 π)3/ V, а мы считаем число состояний на единицу объема (V = 1), для плотности состояний получаем:
зависит только от модуля волнового вектора, то поверхности постоянной энергии в k -пространстве представляют собой сферы (в двумерном пространстве на картинке — круги). Объем тонкого шарового слоя толщиной Δ k равен 4 π k 2 Δ k. Учитывая, что δ k = (2 π)3/ V, а мы считаем число состояний на единицу объема (V = 1), для плотности состояний получаем:
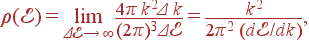
| (10) |
где k 2 и 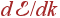 выражены через энергию
выражены через энергию 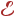 .
.
 2015-05-05
2015-05-05 572
572








