Рассмотрим функцию координат 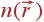 , которая обладает трансляционной симметрией кристалла, например, локальную концентрацию электронов. Трансляционная симметрия функции
, которая обладает трансляционной симметрией кристалла, например, локальную концентрацию электронов. Трансляционная симметрия функции 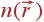 означает, что эта функция не изменяется при сдвиге на произвольный вектор трансляции
означает, что эта функция не изменяется при сдвиге на произвольный вектор трансляции 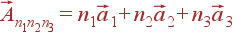 , т. е.
, т. е. 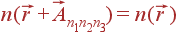 (здесь n 1, n 2, n 3 — целые числа,
(здесь n 1, n 2, n 3 — целые числа, 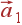 ,
, 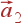 ,
, 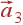 — основные вектора трансляций). Иными словами,
— основные вектора трансляций). Иными словами, 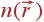 обладает свойством трехмерной периодичности кристалла. Такую функцию можно разложить в ряд Фурье:
обладает свойством трехмерной периодичности кристалла. Такую функцию можно разложить в ряд Фурье:
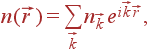
| (23) |
где суммирование ведется по ''разрешенным'' значениям 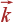 . Выясним, что это за разрешенные значения, т. е. какие
. Выясним, что это за разрешенные значения, т. е. какие 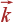 могут присутствовать в разложении. Из свойства периодичности
могут присутствовать в разложении. Из свойства периодичности 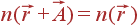 следует:
следует:
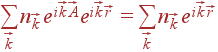
| (24) |
(индексы у вектора трансляции 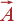 для краткости опускаем).
для краткости опускаем).
Два ряда Фурье равны в том и только том случае, если равны компоненты Фурье этих рядов (равны коэффициенты при  с одинаковыми
с одинаковыми 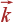 ). Поэтому
). Поэтому

| (25) |
Отсюда следует, что разрешенные 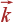 — это любые волновые вектора, удовлетворяющие условию
— это любые волновые вектора, удовлетворяющие условию
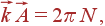
| (26) |
где N — целое число, а 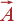 — произвольный вектор трансляции решетки:
— произвольный вектор трансляции решетки:
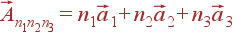
| (27) |
Можно проверить, что условию (26) удовлетворяют все вектора вида
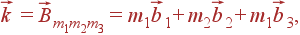
| (28) |
где m 1, m 2, m 3 — целые числа, а 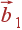 ,
, 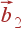 ,
, 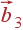 — основные вектора обратной решетки, связанные с основными векторами прямой решетки соотношениями:
— основные вектора обратной решетки, связанные с основными векторами прямой решетки соотношениями:
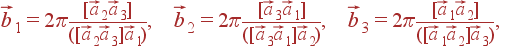
| (29) |
Подведем итоги. Если использовать условия Борна-Кармана, то любая удовлетворяющая этим условиям функция 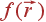 может быть разложена в ряд Фурье:
может быть разложена в ряд Фурье:
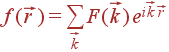
| (30) |
Входящие в эту сумму значения вектора 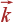 образуют в пространстве векторов
образуют в пространстве векторов 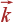 (в обратном пространстве) кубическую решетку с ребром элементарного куба 2 π / L, где L — условная длина (в окончательных результатах L →∞). Эта решетка физического смысла не имеет и введена только для удобства.
(в обратном пространстве) кубическую решетку с ребром элементарного куба 2 π / L, где L — условная длина (в окончательных результатах L →∞). Эта решетка физического смысла не имеет и введена только для удобства.
Для функции, периодической с периодом кристалла, т. е. функции, удовлетворяющей условиям
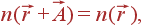
| (31) |
где 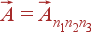 — любой вектор трансляции (вектор прямой решетки), фурье-разложение имеет вид:
— любой вектор трансляции (вектор прямой решетки), фурье-разложение имеет вид:
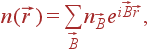
| (32) |
где 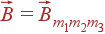 — вектора обратной решетки — вектора удовлетворяющие условиям
— вектора обратной решетки — вектора удовлетворяющие условиям 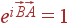 , т. е.
, т. е.
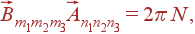
| (33) |
где N — целое число. Нетрудно увидеть, пользуясь формулами (27) и (28), что N = m 1 n 1+ m 2 n 2+ m 3 n 3. Решетка в обратном пространстве, основанная на векторах 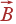 , называется обратной решеткой кристалла. Обратная решетка имеет очень важный физический смысл (см. ниже). В частности, именно на этом понятии основаны закономерности рассеяния рентгеновских лучей.
, называется обратной решеткой кристалла. Обратная решетка имеет очень важный физический смысл (см. ниже). В частности, именно на этом понятии основаны закономерности рассеяния рентгеновских лучей.
Вид обратной решетки определяется видом прямой решетки, например, гранецентрированной решетке Браве соответствует объемоцентрированная обратная решетка. Прямая и обратная решетки обладают одинаковой точечной симметрией.
Объем примитивной ячейки кристалла v 0 — это объем параллелепипеда, построенного на векторах 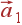 ,
, 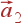 ,
, 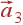 :
:
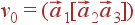
| (34) |
Используя определение векторов 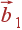 ,
, 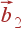 ,
, 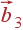 (29), можно найти объем примитивной ячейки обратной решетки:
(29), можно найти объем примитивной ячейки обратной решетки:
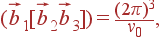
| (35) |
Выше, при рассмотрении граничных условий Борна-Кармана, мы пришли к выводу, что в объеме обратного пространства Δ 3 k содержится 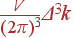 разрешенных состояний волнового вектора (V — объем кристалла). Отсюда следует, что примитивная ячейка содержит
разрешенных состояний волнового вектора (V — объем кристалла). Отсюда следует, что примитивная ячейка содержит
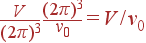
| (36) |
разрешенных состояний волнового вектора, т. е. столько, сколько примитивных ячеек содержит объем кристалла.
 2015-05-05
2015-05-05 1006
1006








