Изоморфизм линейных пространств

Видимая необъятность множества всех n -мерных пространств над данным полем, казалось бы, является препятствием для построения и развития сколько-нибудь общей теории таких пространств.

Оказывается, это не так. Мы сейчас покажем, что над данным полем существует в некотором смысле, лишь одно пространство данной размерности.

Def:Два пространства V и V¢ называются изоморфными, если между их элементами установлено взаимно однозначное соответствие x ↔ x¢. Причем такое, что, если x ↔ x¢, y ↔ y¢, то x + y ↔ x¢ + y¢ и a x ↔a x¢.

24°. Два конечномерных линейных пространства над одним и тем же полем K изоморфны тогда и только тогда, когда dim V = dim V¢.

◀ Необходимость.

а) при изоморфизме q «q ¢. Пусть qÎ V нейтральный элемент в V и x ↔ x¢, q «q ¢. х = q + х «q ¢ + x¢. Учитывая, что x ↔ x¢ Þ q ¢ + x¢ = x¢, т.е. q ¢ нейтрален в V¢.

б) Если V и V¢ изоморфны и { a ₁, …, a_n }↔ { a ¢₁, …, a ¢ _n }, то из линейной независимости { a_i } следует линейная независимость { a ¢ _i }.

Действительно, пусть a₁ a ¢₁+ …+ a _n a ¢ _n =q ¢ ↔a₁ a ₁+ …+ a _n a_n =qÞ a₁= a₂= …= = a _n = 0. Итак, максимальное число линейно независимых векторов в изоморфных пространствах совпадает, т.е. dim V = dim V¢.

Достаточность. Пусть dim V = dim V¢ = n, 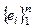– базис в V; 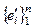, базис в V¢, установим соответствие e ₁↔ e¢ ₁, e ₁↔ e¢ ₂, …, e_n ↔ e¢_n. Тогда x = S a _i e_i ↔ x¢ = S a _i e¢_i; a x = Saa _i e_i ↔ ↔ S aa _i e¢_i = a x¢; x + y = S (a _i + b _i) e_i ↔ S (a _i + b _i) e¢_i . Таким образом, построенное соответствие есть изоморфизм пространств V и V¢. ▶

Итак, изучение всех линейных пространств dim V = n можно свести к изучению А_n – арифметического пространства той же размерности: x Î А_n → x = (a ₁, a ₂, …, a_n).