2015-05-05
638
23°. Пусть V – линейное пространство, dim V = n и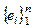 
– базис в V. Тогда " x Î V существует единственный набор 
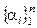, a i ÎK такой, что x = 
.
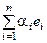◀ Представление x = 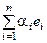следует из полноты .
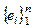Единственность. Пусть 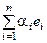x = и x =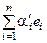 
. Тогда q = x – x = – = = 
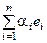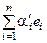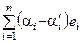и, следовательно, в силу линейной независимости
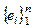, " i a i –a¢ i = 0 т.е. a i =a¢ i. ▶
Теперь ясно, что если в пространстве V задан базис 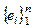, то каждому вектору x Î V можно поставить в соответствие (причем единственным образом) набор чисел a1,a2, …, a n ÎK. Это записывают так: x ↔(a1,a2, …, a n) или x = (a1,a2, …, a n). Величины a i называются координатами вектора x в базисе 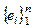. При этом, (что очень важно), если x = (a1,a2, …, a n) и y = (b1, b2, …, b n), то x ⊕ y = (a1 + b1, a2 + b2, …, a n + b n) и g⊙ x = = (ga1, ga2, …, ga n), т.е. операции ⊕и ⊙ заменены покоординатным сложением и умножением на элемент внешнего поля K.
Другими словами, введение понятия базиса векторного пространства V над полем K и координат векторов в этом базисе абстрактные операции сложения для элементов линейного пространства и умножения их на скаляры из внешнего поля K позволяет свести к операциям покоординатного сложения и умножения на скаляр, т. е. к умножению и сложению в поле K.
