НормИРОBАНные пространства

Сосредоточив внимание на таком свойстве множества, как наличие в нем расстояния приходим к понятию метрического пространства.

Сосредоточив внимание на операциях в множестве приходим к понятию линейного пространства.

Если каждое расстояние никак ни связанно с операциями над элементами, то представляется весьма затруднительным построить содержательную теорию части которой соединяли бы вместе алгебраические и метрические понятия.

Поэтому мы будем на метрику, введенную в линейном пространстве накладывать дополнительные условия.

Вещественное или комплексное линейное пространство Х называется нормированным пространством, если для любого х Î Х существует вещественное число || х || называемое нормой вектора х такое, что выполняются следующие аксиомы (аксиомы нормы):

А) || х || ≥ 0 причем || х || = 0 Û х = θ (положительность нормы);

В) ||λ х || = |λ| || х || (абсолютная однородность нормы);

С) || х + у || ≤ || х || + || у || (неравенство треугольника).

Примеры норм. Если вектор х в некотором базисе имеет координаты х = (х ₁, х ₂, …, х _n), то: a) || х ||_l = 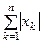; b) || х ||₂ = 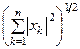; g) || х || _p = 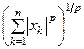; d) || х || = 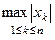. Норма b) называется евклидовой нормой.