7°. Нормированное пространство легко превратить в метрическое, вводя r(х, у) = || х – у ||. В самом деле:
◀ А) r(х, у) = || х – у || = ||(–1)(у – х) || = |–1| || у – х || = || у – х || = |–1| || у – х || = || y – x || = r(y, x);
В) r(х, у) = || х – у || ≥0, причем || х – у || = 0 Û x – y = θ Û x = y;
С) r(х, у) = || х – у || = ||(x – z) + (z – y)|| ≤ || x – z || + || z – y || = r(х, z) + r(z, у). ▶
Отметим что || х || = r(х, θ).
Обратим внимание, что метрика в линейном пространстве обладает свойствами:
А) r(х + z, у + z) = r(х, у) – расстояние не меняется при сдвиге;
В) r(λ х, λ у)= |λ|r(х, у) – расстояние есть абсолютно однородная функция. (**)
8°. Если в метрическом линейном пространстве Х метрика удовлетворяет двум последним (**) требованиям, то Х можно превратить в нормированное пространство, вводя || х || = r(х, θ).
◀ А) || х || = r(х, θ) ≥0; || х || = r(х, θ) = 0 Û x = θ;
В) ||λ х || = r(λ х, θ) = r(λ х, λθ) = |λ|r(х, θ) = |λ| || х ||;
С) || х – у || = r(х + y, θ) = r(х + y – y, θ – y) = r(х,– y) ≤ r(х, θ) + r(θ,– y) =
= r(х, θ) + |–1|r(y, θ) = || х || + || у ||. ▶
9°. Линейное пространство со скалярным произведением является нормированным (|| х || = 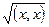 ) и метрическим (r(х + y) = || х – у ||) пространством. ◀ ▶
) и метрическим (r(х + y) = || х – у ||) пространством. ◀ ▶
Покоординатная сходимость
 2015-05-05
2015-05-05 354
354








