Квадратичная форма

Если в билинейной форме j(х, у) положить у = х, то получим частный случай билиней­ной формы – квадратичную форму j(х, х).

Представив билинейную форму j(х, у) в виде суммы симметрической и антисимметри­ческой билинейных форм, получим:

.

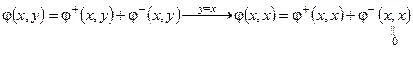Отсюда, ясно, что каждой билинейной форме однозначно ставится в соответствие квадратичная форма (ее матрица симметричная), но не наоборот. Т.е., в общем случае, по имеющейся квадратичной форме нельзя однозначно восстановить билинейную форму, из которой она получена. НО …

2°. Для каждой квадратичной формы существует, и при том только одна, симметричная били­нейная форма, из которой получена данная квадратичная форма. (Эта симметричная били­нейная форма называется полярной к заданной квадратичной форме).

◀ j(х + у, х + у) = j(х, х) + j(у, х) + j(х, у) + j(у, у) если j(х, у) = j(у, х), то

j(х + у, х + у) = j(х, х) + 2j(х, у) + j(у, у), т.е. j(х, у) = 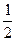{j(х + у, х + у) – j(х, х) – j(у, у)}. ▶