Рассмотрим произвольную дифференцируемую функцию f на некоторой гладкой поверхности S. Точка х 0Î S называется стационарной (критической) точкой, если в x 0 производная f по любому направлению на поверхности S равна нулю.
Мы исследуем вопрос о стационарных (в частности экстремальных) точках и значениях квадратичной формы B (x, x) на сфере единичного радиуса в евклидовом пространстве V и о связи этих значений с собственными векторами и значениями самосопряженного оператора А, такого, что (Ax, y) = B (x, y). При этом единичной сферой в V назовем множество х Î V для которых (x, x) = || x || = 1.
Итак: пусть B (x, x) – квадратичная форма, B (x, y) – полярная ей симметричная билинейная форма, A – самосопряженный оператор: B (x, y) = (Ax, y), тогда в базисе из собственных векторов оператора А: 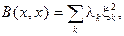 здесь λ k – собственные значения А.
здесь λ k – собственные значения А.
Договоримся, что l1 ³ l2 ³ l3 ³ l4 ³ … ³ l n. Заметим, что в выбранном базисе уравнение единичной сферы таково: 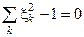 .
.
Т°. Стационарные значения квадратичной формы B (x, x) на единичной сфере равны
собственным значениям λ k оператора А. Эти стационарные значения достигаются на единичных собственных векторах еk оператора А.
Задача: найти точки экстремума B (x, x) при условии (x, x) = 1. Этo задача на условный экстремум.
◀ Можно воспользоваться методом неопределенных множителей Лагранжа.
Функция Лагранжа: 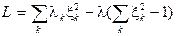 . Н еобходимое условие экстремума:
. Н еобходимое условие экстремума: 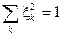 и
и 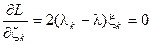 , k = 1, 2, …, n.
, k = 1, 2, …, n.
Здесь l k – неопределенные множители Лагранжа.
Решение этой системы: 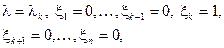 т.е. эти решения – собственные значения и собственные векторы оператора А.
т.е. эти решения – собственные значения и собственные векторы оператора А.
Примечание: Числа λ1 и λ n являются собственно наибольшим и наименьшим значением B (x, x) на сфере (x, x) = 1, т.е. 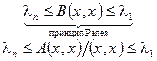 ,
, 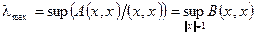
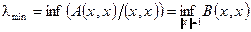 .
.
Неравенства 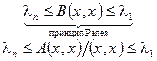 характеризуют, так называемый, принцип Рэлея. При этом,
характеризуют, так называемый, принцип Рэлея. При этом, 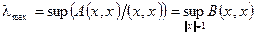 ,
, 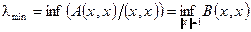
Для нахождения наибольшего по модулю собственного значения оператора А, можно применить следующую процедуру:. 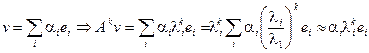 ;
; 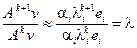 ;
; 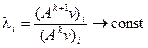 .
.
 2015-05-05
2015-05-05 541
541







