2015-05-05
602
1) Аддитивные группы: {0}, Q, R, C, множество Zk целых чисел, кратных целому заданному k.
2) 
Мультипликативные: {1}, {1, –1}, {1, i, –1, – i }, множество { z Î C ½|| z || = 1}, P + – множество вещественных положительных чисел, Q \{0}, R \{0}, C \{0}.
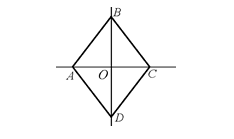
3) Группа симметрий ромба V: { E, SBD, SAC, S 0}.
Таблица Кэли:
| E | SBD | SAC | S0 | |
| E | E | SBD | SAC | S0 |
| SBD | SBD | E | S 0 | SAC |
| SAC | SAC | S 0 | E | SBD |
| S 0 | S 0 | SAC | SBD | E |
4) Для заданного равностороннего треугольника АВС рассмотрим преобразования, отображающие треугольник сам на себя:
1. Е – тождественное преобразование.
2. α – поворот на угол 2π/3 против часовой стрелки.
3. β – поворот на угол 4π/3 против часовой стрелки.
4. S 1 – симметрия относительно оси (1) (В 
С)
5. S 2 – симметрия относительно оси (2) (А С)
6. S 3 – симметрия относительно оси (3) (А В).
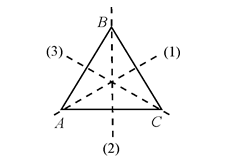Закон композиции зададим таблицей Кэли:
| II ⊙ I | E | a | b | S 1 | S 2 | S 3 |
| E | E | a | b | S 1 | S 2 | S 3 |
| a | a | b | E | S 2 | S 3 | S 1 |
| b | b | E | a | S 3 | S 1 | S 2 |
| S 1 | S 1 | S 2 | S 3 | E | a | b |
| S 2 | S 2 | S 3 | S 1 | b | E | a |
| S 3 | S 3 | S 1 | S 2 | a | b | E |
Такой закон композиции ассоциативен, но не коммутативен (например S 1⊙ S 2¹ S 2⊙ S 1. Единичный элемент Е – тождественное преобразование, обратные a-1 = b; b-1 = a;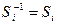 
.
|
|
|
Множество преобразований самосовмещения треугольника с таким законом композиции называется группой самосовмещений равностороннего треугольника.
Подмножество { E, a, b} этой группы образует подгруппу группы самосовмещений и называется группой поворотов равностороннего треугольника.
5) Перестановкой назовем закон, по которому элементам a, b, c, d, … взаимно однозначно ставятся в соответствие элементы того же множества, но, возможно, в другом порядке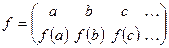 
.
Композиция двух перестановок f 1⊙ f 2 определяется как последовательное применение двух перестановок: сначала f 2, а потом f 1.
Для конечного множества Е из n – элементов перестановки образуют группу (не абелевую!), которая называется симметричной группой Sn.
В частности:
Группа перестановок трех элементов S 3:
Пусть P 1=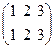 
, P 2 = 
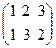, P 3 = 
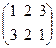, P 4 = 
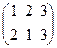, P 5 = 
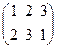, P 6 = 
.
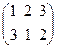Закон композиции определен таблицей:
| P 1 | P 2 | P 3 | P 4 | P 5 | P 6 | |
| P 1 | P 1 | P 2 | P 3 | P 4 | P 5 | P 6 |
| P 2 | P 2 | P 1 | P 5 | P 6 | P 3 | P 4 |
| P 3 | P 3 | P 6 | P 1 | P 5 | P 4 | P 2 |
| P 4 | P 4 | P 5 | P 6 | P 1 | P 2 | P 3 |
| P 5 | P 5 | P 4 | P 2 | P 3 | P 6 | P 1 |
| P 6 | P 6 | P 3 | P 4 | P 2 | P 1 | P 5 |
Данная группа имеет три подгруппы по два элемента: { P 1, P 2}, { P 1, P 3}, { P 1, P 4} и одну подгруппу из трех элементов: { P 1, P 5, P 6}.
Группу самосовмещений равностороннего треугольника можно представить как группу перестановок трех элементов:
.
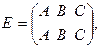
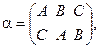
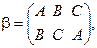
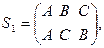
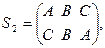
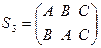6) Рассмотрим множества, состоящие из двух элементов {0, 1} с операцией: 0⊙0 = 0; 0⊙1 = 1; 1⊙0 = 1; 1⊙1 = 1. Единичный элемент здесь 0.
Эта группа называется группой вычетов по модулю 2 и обозначается Z 2.
|
|
|
7) Группа из двух преобразований евклидового пространства: а) тождественное преобразование – 0, б) отражение относительно θ – 1.
От группы Z 2 – отличается лишь природой элементов, групповые свойства одинаковы.
