Банк до наступления срока платежа по векселю или иному платежному обязательству приобретает его у владельца по цене, которая меньше суммы, указанной на векселе, т.е. покупает (учитывает) его с дисконтом (т.е. со скидкой). В данном случае дисконт и является процентным доходом. Владелец векселя при учете векселя имеет возможность получить деньги ранее указанного на нем срока, хотя и не в полном объеме.
При учете векселя применяется банковский (коммерческий) учет. Проценты (в форме дисконта) за пользование ссудой начисляются по учетной ставке на сумму, подлежащую уплате в конце срока.
P = S – Snd = S (1 – nd), (3.7)
где P – сумма, по которой вексель учитывается;
S – сумма, на которую вексель выдан;
n – срок от момента погашения до даты погашения векселя;
d – учетная ставка (в долях единицы);
Snd – дисконт (сумма учета).
Формула (2.7) – формула дисконтирования по учетной ставке процента.
(1 – nd) – дисконтный множитель.
В данном случае говорят, что сумма S дисконтируется (учитывается), сам процесс начисления процентов и их удержания называется учетом, а удержанные проценты – дисконтом (скидкой).
Математическое дисконтирование – установление современной величины P суммы S, выплачиваемой через период n. Данная задача является обратной наращению.
Для ставки наращения прямой задачей является определение наращенной суммы, обратной – дисконтирование. Для учетной ставки, наоборот, прямая задача заключается в дисконтировании, обратная – в наращении.
| Ставка | Прямая задача | Обратная задача |
| i | S = P (1 + ni) | 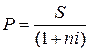
|
| d | P = S (1 – nd) | 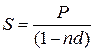
|
Очевидно, что даже при равенстве ставки наращения i и учетной ставки d рассмотренные два метода приводят к разным результатам.
Учетная ставка отражает фактор времени гораздо более жестко, причем, чем выше ставка, тем больше влияние этого фактора.
| Вид ставки | Формула | Срок, n | |||||
| 1/12 | 1/4 | 1/2 | |||||
| Дисконтные множители, i = d = 20% | |||||||
| i | 1/(1+ ni) | 0,9836 | 0,9524 | 0,9091 | 0,8333 | 0,7143 | 0,3333 |
| d | (1– nd) | 0,9833 | 0,9500 | 0,9000 | 0,8000 | 0,6000 | – |
| Множители наращения, i = d = 20% | |||||||
| i | (1+ ni) | 1,0167 | 1,0500 | 1,1000 | 1,2000 | 1,4000 | |
| d | 1/(1– nd) | 1,0169 | 1,0526 | 1,1111 | 1,2500 | 1,6667 | – |
 2015-05-05
2015-05-05 732
732








