Задача о замке

В качестве примера рассмотрим комбинационный замок допустим для вело­сипеда, состоящий из набора N переключателей, каждый из которых может быть в положении «вкл» или «выкл». Замок открывается только при одном наборе положений переключателей, из которых не менее [N/2] (целая часть от N/2) находятся в положении «вкл». Предпо­ложим, что мы забыли эту комбинацию, а нам надо отпереть замок. Предположим также, что мы готовы перепробовать (если необходимо) все комбинации. Нам нужен алгоритм для систематического генери­рования этих комбинаций. Если проигнорировать условие [N/2], то для замка существует 2^N возможных комбинаций. Однако условие [N/2J позволит отбросить (или лучше не генерировать) многие комбинации.

Промоделируем каждую возможную комбинацию вектором из N нулей и единиц. На i-м месте будет 1, если i-й переключатель нахо­дится в положении «вкл», и 0, если i-й переключатель — в положении «выкл». Множество всех возможных N-векторов хорошо моделируется с помощью двоичного дерева. Каждая вершина k-го уровня этого дерева будет соответствовать определенному набору первых k компонент N-вектора. Две ветви, идущие вниз из вершины этого уровня, соответствуют двум возможным значениям (k+1)-й компоненты в N-векторе. У дерева будет N уровней. Рис. 5.5 на примере N=4 поясняет основную конструкцию.

Условие, заключающееся в том, что число переключателей в положении «вкл» должно быть не меньше [N/2], позволяет нам не образовывать части дерева, которые не могут привести к правильной комбинации. Например, рассмотрим вершину 00 на рис. 5.5. Так как правая ветвь (к 000) не может привести к допустимой комбинации, нет нужды ее формировать. Если какие-то вершины, следующие за рассматриваемой вершиной, не удовлетворяют ограничению задачи, то эти вершины не надо рассматривать. В данном случае никакие из вершин, находящихся внутри пунктирных линий, не нужно исследо­вать и даже формировать.

Теперь, воспользовавшись этой моделью двоичного дерева, можно изложить процедуру отхода назад для образования только тех ком­бинаций, в которых по крайней мере [N/2] переключателей нахо­дятся в положении «вкл». Алгоритм сводится к пересечению дерева.

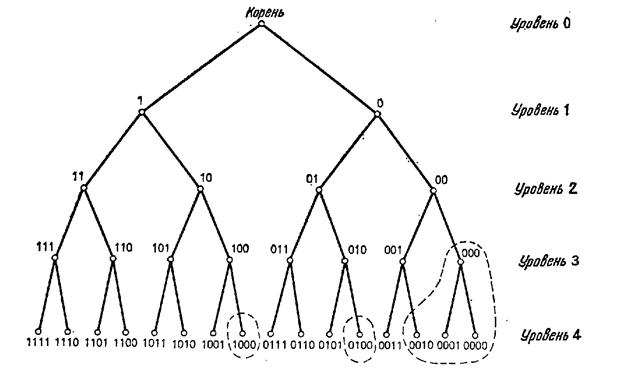
Рис. 5.5 Двоичное дерево, представляющее N-векторы из нулей и единиц.

Двигаемся вниз по дереву, придерживаясь левой ветви, до тех пор, пока это возможно. Достигнув конечной вершины, опробуем соот­ветствующую комбинацию.. Если она не подходит, поднимаемся на один уровень и проверяем, можем ли мы спуститься опять по другой ветви. Если это возможно, берем самую левую из неисследованных ветвей. Если нет, отходим вверх еще на один уровень и пытаемся спуститься из этой вершины. Перед спуском проверяем, можно ли удовлетворить условие об [N/2] включенных переключателях в последующих вершинах. В ситуации, изображенной на рис. 5.5, этот алгоритм просмотрит следующую последовательность вершин:

1111 Проверка этой комбинации.

0111 Отход, так как 1111 —конечная вершина.

1110 Спуск по единственной непросмотренной ветви вниз, про­верка этой комбинации.

0111 Снова отход.

0011 Отход дальше, так как из 0111 все ветви просмотрены.

0110 Спуск по единственной непросмотренной ветви.

1101 Проверка комбинации.

0110 Отход из 1101

1100 Проверка комбинации.

0110 Отход из 1100.

0011 Отход, так как все ветви просмотрены.

0001 Отход, так как все ветви просмотрены.

0010 Спуск по единственной непросмотренной ветви.

0101 Спуск по самой левой непросмотренной ветви.

1011 Проверка комбинации.

0101 Отход.

1010 Проверка комбинации.

0101 Отход.

0010 Отход.

0100 Спуск по единственной непросмотренной ветви.

1001 Проверка комбинации.

0100 Отход.

0010 Отход; заметим, что мы не опускаемся к 1000, так как эта вершина нарушает условие о том, что должно быть по край­ней мере две единицы.

0001 Отход.

Корень Отход.

0 Спуск по единственной непросмотренной ветви.

.

.

.

и т. д.

Алгоритм останавливается, когда мы возвращаемся к корню и не остается непросмотренных ветвей.

Этот простой пример иллюстрирует основные свойства, общие для всех алгоритмов с отходом назад. Если можно сформулировать задачу так, что все возможные решения могут быть образованы построением N-векторов, тогда ее можно решить при помощи процедуры с отходом.

5.4. Метод ветвей и границ

Метод, известный как метод ветвей и границ, похож на методы с отходами назад тем, что он исследует древовидную модель простран­ства решений и применим для широкого круга дискретных комбина­торных задач. Алгоритмы с отходами нацелены на то, чтобы найти одну или все конфигурации, моделируемые N-векторами, которые удовлетворяют определенным свойствам. Алгоритмы ветвей и границ ориентированы в большей степени на оптимизацию.

В этом методе определяется некая функция, как весовая числовая функция для различных вариантов решения задачи и вычисляется численные значения этой функции для различных вариантов решения. Цель — найти конфигурацию, на которой эта функция достигает максимального или минималь­ного значения. Сам же метод отыскания и построения такой функции получил название метод ветвей и границ. Такое название возникло в результате того, что в нем используется ветвление и вычисляются границы.

Рассмотрим более подробно что понимается под ветвлением и что понимается под границей.

Ветвление - это процесс разбиения всех вариантов решения задачи на два множества, таким образом, что какая-либо конкретная подзадача принадлежит только одному из этих множеств. В этом случае говорят, что ветвление происходит на этой подзадаче. Если пользоваться терминологией древовидной структуры, то говорят, что ветвление происходит на определенной ветви древовидной структуры.

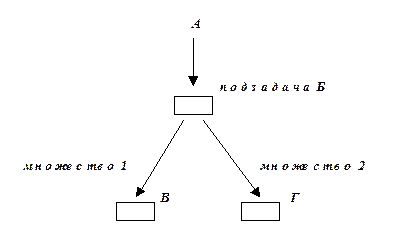Рис.5.6

На рис 5.6 показана древовидная структура, ветвление производится в точке Б при рассмотрении подзадачи Б, дальнейшее решение задачи пойдет либо по пути Б-В, либо по пути Б-Г. Ветвление происходит в точке Б и разбивается на два подмножества. Сущность ветвления заключается в том, что какая-то конкретная подзадача Б входит в множество 1 и не входит в множество 2 вариантов решения задачи.

Следующим шагом является вычисление нижних границ. Под этим понимается вычисления весовой функции для всей вариантов множества 1 или множества 2. Для каждого множества 1 или 2 существует конечное число вариантов решения, в которых весовая функция принимает определенные значения. Назовем из множество значений весовой функции 1 и 2, которые соответствуют множествам 1 и 2. Естественно, что для каждого из множеств весовой функции имеется определенная граница нижняя или верхняя, по которой происходит оценка дальнейшего пути решения задачи.

Другими словами, если нам необходимо минимизировать весовую функция и удалось доказать, что нижняя граница этой функции для множества 1 меньше чем нижняя граница из множества 1, то необходимо продвигаться по пути Б-В решения задачи.

Поясним это на примере.

Как конкретно определить подзадачу ветвления рассмотрим на примере транспортной задачи с коммивояжером, в которой очень хорошо работает алгоритм ветвей и границ. В данном разделе изложение будет вестись на примере этой задачи. Сделаем замечание, что алгоритмы ветвей и границ, как правило, бывают довольно сложны и представленный здесь — не исключение. Тем не менее, в некоторых случаях, его использование бывает очень эффективным. При помощи алгоритмов ветвей и границ удалось решить большой круг разнообразных серь­езных практических задач, но эти алгоритмы редко оказыва­ются простыми.

Напомним, что задача заключается в нахождении в торговом участке коммивояжера пути из N городов с наименьшей стоимостью. Каждый город входит в путь только один раз. В терминах сетей в сети городов надо найти покрывающий цикл наименьшей стоимости. Имеется матрица С, каждый элемент которой Сij равен стоимости (обычно в единицах времени, денег или расстояния) прямого проезда из города I в город J. Задача называется симметричной, если Сij=Cji для всех i и j, т. е. если стоимость проезда между каждыми двумя городами не зависит от направления. Предположим, что Сii = ¥ для всех i.

Алгоритмы ветвей и границ для задачи коммивояжера могут быть сформулированы разными способами. Авторы излагаемого алгорит­ма — Литл, Мерти, Суини и Карел. Это своего рода классика.

Во-первых, рассмотрим ветвление. На рис. 5.7а показана мат­рица стоимостей для асимметричной (несимметричной) задачи комми­вояжера с пятью городами, представленной на рис.5.7б. Обратите внимание на то, что мы пользуемся направленной сетью, чтобы ука­зать стоимости, так как стоимость проезда из города i прямо в город j не обязательно такая же, как стоимость проезда из города j в город i. Корень нашего поискового дерева будет соответствовать множеству «всех возможных вариантов», (в дальнейшем назовем каждый вариант решения задачи туром) т. е. эта вершина представляет множество всех 4! возможных туров в нашей задаче с пятью городами. В общем случае для любой асимметричной задачи с N городами корень будет представлять полное множество R всех (N—1)! возможных туров. Ветви, выходящие из корня, определяются выбором одного ребра, скажем (i, j).

Наша цель состоит в том, чтобы разделить множество всех туров на два множества: одно, которое, весьма вероятно, содер­жит оптимальный тур, и другое, которое, вероятно, не содержит. Для этого выбираем ребро (i,j); оно, как мы надеемся, входит в оп­тимальный тур, и разделяем R на два множества {i,j} и {i,j}. В мно­жество {i, j} входят туры из R, содержащие ребро (i, j), а в {i,j} — не содержащие (i,j).

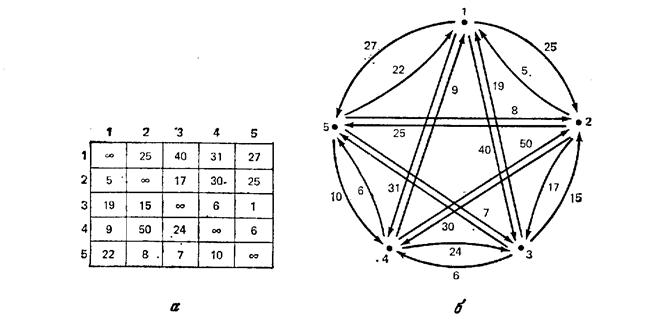
Рис. 5.7 Задача коммивояжера: (а) матрица стоимостей; (б) сеть из пяти городов.

Предположим, в нашем примере мы производим ветвление на ребре (i, j) = (3,5), имеющем наименьшую стоимость во всей матрице. Корень и первый уровень дерева пространства решений будут тогда такими, как показано на рис.5.8 Заметим, что каждый тур из R содержится только в одном множестве уровня 1. Если бы мы как-то могли сделать вывод, что множество {3,5} не содержит оптимального тура, то нам нужно было бы исследовать только множество {3, 5}.

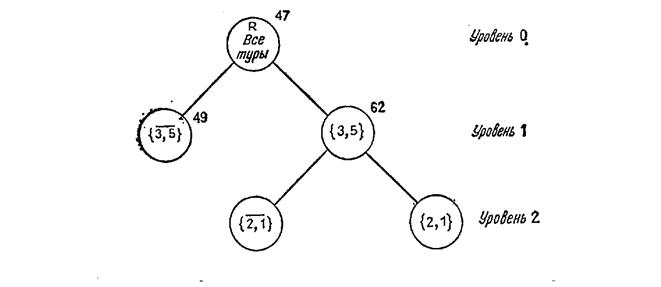
Рис. 5.8. Построение дерева поиска по методу ветвей и границ.

Затем разделяем множество {3, 5} таким же образом, как и множе­ство R. Следующее по дешевизне ребро в матрице — это ребро (2, 1) со стоимостью 5. Поэтому можно разделить множество {3, 5} на туры, включающие ребро (2, 1), и туры, не включающие этого ребра; это показано на уровне 2 на рис. 5.8. Путь от корня к любой вершине дерева выделяет определенные ребра, которые должны или не должны быть включены в множество, представленное вершиной дерева. Например, левая вершина уровня 2 на рис. 5.8 представляет множе­ство всех туров, содержащих ребро (3, 5) и не содержащих ребра (2, 1). Вообще, если Х — вершина дерева, a (i, j) — ребро ветвления, то обозначим вершины, непосредственно следующие за X, через Y и Y. Множество Y обозначает подмножество туров из Х с ребром (i,j), а множество Y — подмножество Х без (i, j).

Теперь, когда на примере мы пояснили, что такое ветвление, поясним, на этом же примере что подразумевается под вычислением границ.

Для каждой вершины дерева существует определенное множество решений, это множество укладывается в некоторые границы. Решения задачи мы связывает с весовой функцией. Для нашего случая эта функция представляет собой общую стоимость проезда. И поскольку для каждой вершины дерева может быть определенное множество решений, следовательно, для каждой вершины имеется определенное множество значений функций стоимости. Это множество значений имеет границы - верхнюю и нижнюю. Для нашей задачи о минимальной стоимости проезда, нас будет интересовать нижняя граница функции стоимостей.

Вычис­ление этих нижних границ — основной фактор, дающий экономию усилий в любом алгоритме типа ветвей и границ. Поэтому особое внимание следует уделить получению как можно более точных границ. Причина этого следующая. Предположим, что мы получили нижнюю границу стоимостей на одной вершине m, а на другой М и выполняется условие М>m, то исследованию должна быть подвергнута вершина стоимости m. и все следующие за ней.

Основной шаг при вычислении нижних границ известен как при­ведение. Оно основано на следующих двух соображениях:

1. В терминах матрицы стоимостей С каждый полный тур содержит только один элемент (ребро и соответствующую стоимость) из каждого столбца и каждой строки. Заметим, что обратное утверждение не всегда верно. Множество, содержащее один и только один элемент из каждой строки и из каждого столбца С, не обязательно представ­ляет тур. Например, в задаче, изображенной на рис. 5.7, множе­ство {(1, 5), (5, 1), (2, 3), (3, 4), (4, 2)} удовлетворяет этому условию, но не образует тура.

2. Если вычесть константу h из каждого элемента какой-то строки или столбца матрицы стоимостей С, то стоимость любого тура при новой матрице С' ровно на h меньше стоимости того же тура при матрице С. Поскольку любой тур должен содержать ребро из данной строки или данного столбца, стоимость всех туров уменьшается на h. Это вычитание называется приведением строки (или столбца).

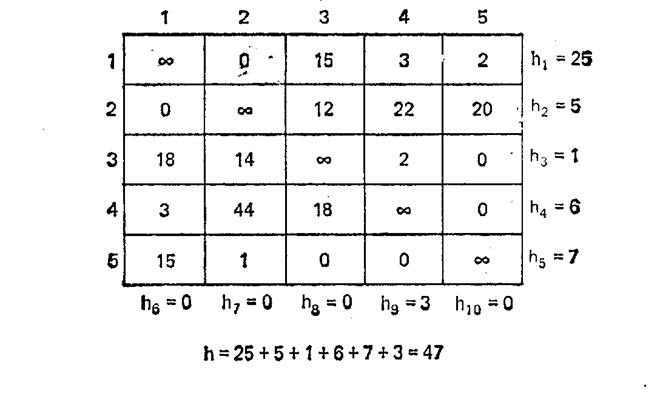
Рис. 5.9. Приведение матрицы стоимостей, показанной на рис.5.7 а.

Под приведением всей матрицы стоимостей С понимается следую­щее. Последовательно проходим строки С и вычитаем значение наи­меньшего элемента Hi каждой строки из каждого элемента этой строки. Потом то же самое делаем для каждого столбца. Если для некоторого столбца или строки Hi=0, то рассматриваемый столбец или строка уже приведены, и тогда переходим к следующему столбцу или строке.

Сумма всех Hi есть нижняя граница стоимостей, обозначим ее как H

Полученную в результате матрицу стоимостей назовем приведенной из С. На рис.5.9 показано приведение матрицы стоимостей, изобра­женной на рис. 5.7а. Значения Hi, даны в конце каждой строки и столбца (строки и столбцы последовательно перенумерованы).

Общее приведение составляет H=47 единиц. Следовательно, ниж­няя граница стоимости любого тура из R также равна 47. Эта граница указана около корня дерева на рис. 5.8. Рассмотрим нижние границы для вершин уровня 1, т. е. для множеств {3,5} и {3,5}. Вычислим их нижние границы.

По определению ветвления путь (3,5) содержится в каждом туре множества {3,5}, следовательно путь (5,3) в нем не может содержаться, исходя из условий задачи (поездка осуществляется по одному пути только один раз) и, поэтому, значение (5,3) в матрице стоимостей равно бесконечности. Строку 3 и столбец 5 также можно исключить из дальнейшего рассмотрения потому что путь (3,5) уже существует. (строка 3 предполагает выезд из 3, а столбец 5 приезд в 5). Таким образом матрица приведенная на рис. 5.9. может быть нарисована в виде, изображенном на рис. 5.10. На рис.5.10а показана матрица после вычеркивания из нее строки 3 и столбца 5 и соблюдения условия, что стоимость (5,3) равна бесконечности, а на рис.5.10б показана уже приведенная матрица.

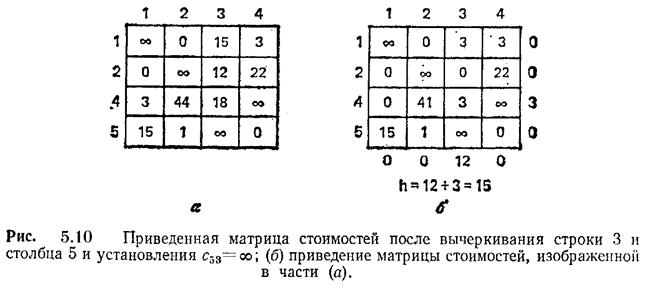
Нижняя граница для множества {3,5} равна сумме Н для предыдущего значения 47 и полученного 15, т.е. нижняя граница равна 62.

Нижняя граница множества {3,5} получается несколько иным способом. Путь (3,5) не может находится в этом множестве, поэтому полагаем его равным бесконечности (для матрицы расположенной на рис.5.9). Но в любой вариант решения задачи будет входить путь из 3 в какой либо другой город и путь входящий в город 5 из какого либо другого города. Выбираем минимальные значения стоимостей для этих путей. Самое меньшее из города 3 равно 2 (полагая (3,5) бесконечности), а самое меньшее входящее в 5 равно 0. Следовательно нижняя граница равна 47+2=49.

Значения 62 и 49 указаны на рис. 5.8. Естественно, что теперь необходимо рассматривать множество {3,5}.

В основных чертах блок-схема этого алгоритма ветвей и границ показана на рис.5.11.

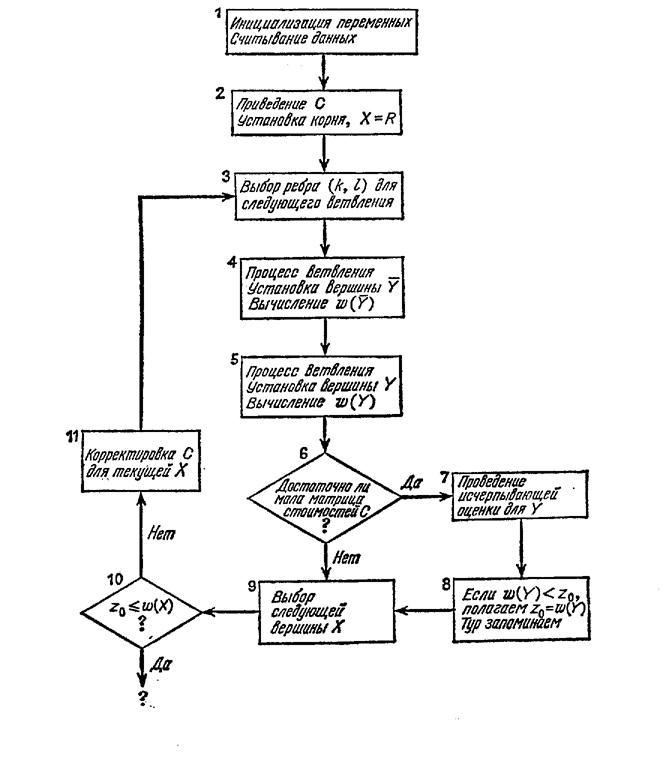
Рис. 5.11 Блок-схема алгоритма ветвей и границ.

Здесь используются следующие обозначения. Буква Х обо­значает текущую вершину на дереве поиска, a w (X) — соответствующую нижнюю границу. Вершины, следующие непосредственно за X, назовем Y и Y, они выбираются ветвлением по некоторому ребру (k, l). Символ Zo обозначает стоимость самого дешевого варианта, извест­ного на данный момент. В начальный момент Zo =oo.

Теперь раскроем более детально содержание некоторых блоков этой схемы.

Блок 1. Установление начальных значений переменных, или ини­циализация.

Блок 2. Первое приведение — это непосредственная реализация описанной ранее процедуры.

Блок 3. Выбор следующего ребра ветвления (k, 1) определяет множества Y и Y, непосредственно следующие за текущим X. Ребро (k, 1) нужно выбирать так, чтобы попытаться получить большую по величине нижнюю границу на множестве Y={k, 1), что облегчит проведение оценки для множества Y. Обычно предпочтительнее про­вести оценку для Y, так как размер этого множества и соответству­ющая ему матрица стоимостей обычно больше, чем у Y (из матрицы для Y вычеркнуты строка k и столбец l). Можно надеяться также, что Y с большей вероятностью содержит оптимальный вариант.

Как применить эти идеи к выбору конкретного ребра ветвления (k, l). В приведенной матрице стоимостей С, связанной с X, каждая строка и столбец имеют хотя бы по одному нулевому элементу (если нет, то С не полностью приведена). Можно предположить, что ребра, соответствующие этим нулевым стоимостям, будут с большей веро­ятностью входить в оптимальный вариант, чем ребра с большими стои­мостями. Поэтому мы выберем одно из них. Но какое? Пусть ребро (i,j) имеет Cij=0 в С. Мы хотим, чтобы у Y = {i, j) была как можно большая нижняя граница. Вспоминая метод вычисления нижней границы для {3, 5} в нашем примере, мы видим, что для Y эта граница задается в виде

W(Y)=w(X)+ (наименьшая стоимость в строке i, не включая Cij)+(наименьшая стоимость в столбце j, не включая Сij).

Следовательно, из всех ребер (i, j) с Cij=0 в текущей матрице С мы выбираем то, которое дает наибольшее значение для W(Y).

Учитывая, что данный метод довольно трудный для понимания ниже приводится решение транспортной задачи с указанными выше данными.