Задача о вертолете

Мы хотели бы сделать перелет на легком вертолете через пустыню, которая тянется на 1000 километров, израсхо­довав при этом минимум горючего. Максимальный объем горючего, которое может захватить с собой вертолет, предположим, составляет 500 литров, горючее расходуется равномерно, по 1 литру на километр. В точке старта имеется неограниченный резервуар с топливом. Так как в пустыне нет складов горючего, мы должны установить свои соб­ственные хранилища и наполнить их топливом. Задача будет решена, если мы ответим на следующие вопросы. Где расположить эти хранилища? Сколько горючего нужно залить в каж­дое из них?

Подойдем к этой задаче с помощью метода отрабатывания назад. На какое расстояние от конца мы сможем пересечь пустыню, имея за­пас горючего в точности на k баков? Мы будем задавать этот вопрос для k=1, 2, 3,..., пока не найдем такое целое п, что п полных баков позволят пересечь всю 1000-километровную пустыню.

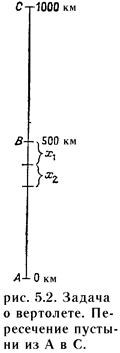
Для k=1 ответ равен 500 милям, как и показано на рис. 5.2. Можно заправить машину в точке В и пересечь оставшиеся 500 километров пустыни. Ясно, что это наиболее отдаленная точка, стартуя из которой можно преодолеть пустыню, имея в точности 500 литров горючего.

Мы поставили перед собой частную цель, потому что не смогли бы решить сразу исходную задачу. Мы не задаем вопрос: сколько топлива нужно вертолету, чтобы преодолеть заданную дистанцию? Вместо этого задаем более простой, но родственный вопрос: какое расстояние можно пролететь на заданном количестве топлива? Ответить на первый вопрос становится воз­можным, когда ответом на второй является: не мень­ше 1000 километров.

Предположим, что k=2, т. е. имеется два полных бака (1000 литров). Будем рассматривать этот слу­чай, опираясь на результат для k=1. Данная ситуа­ция иллюстрируется на рис. 5.2. Каково максималь­ное значение X₁, такое, что, отправляясь с 1000 литрами горючего из точки 500— X₁, можно перевезти горючего в точку В столько, чтобы из точки В мы вылетели с 500 литрами горючего (т.е. как в случае k=1).

Один из способов определения приемлемого зна­чения Xi состоит в следующем. Заправляемся в точ­ке 500—X₁, едем X₁ километров до В и переливаем в хранили­ще все горючее, кроме X₁ литров, которые потребуют­ся для возвращения в точку 500-X₁. В этой точке бак становится пус­тым. Теперь наполняем его снова, проезжаем X₁ километров до В, забираем в В горючее, оставленное там, и из В едем в С с полным ба­ком. Общее пройденное расстояние состоит из трех отрезков по X₁ километров и одного отрезка ВС длиной 500 километров. Мы должны израсходовать каждую каплю топлива, чтобы сделать значение X₁ как можно боль­шим. Поэтому X₁ находим из уравнения

3 Õ₁ + 500 =1000 (литров);

его решение: Õ₁=500/3.

Таким образом, два бака (1000 литров) позволяют нам пролететь расстояние

D₂=500+X₁=500 (l+1/3) километров.

Заметим, что исходная предпосылка является недальновидной и грубой. Когда имеются в распоряжении k баков горючего, мы просто стараемся продвинуться назад как можно дальше от точки, найденной для k—1 баков.

Рассмотрим k=3. Из какой точки мы можем вылететь с 1500 литрами топлива так, что вертолет сможет доставить 1000 литров в точку 500—X₁? Возвращаясь к рис. 5.2, мы ищем наибольшее значение Х₂, такое, что, выезжая с 1500 литрами топлива из точки 500—X₁—Х₂, мы можем доставить 1000 литров в точку 500—X₁. Мы выезжаем из точки 500—X₁—Х₂, доезжаем до 500—X₁, переливаем все горючее, кроме Х₂ литров, и возвращаемся в точку 500—X₁—Х₂ с пустым баком. Повторив эту процедуру, мы затратим 4Х₂ литров на проезд и оставим 1000 — 4Х₂ литров в точке 500—X₁. Теперь в точке 500—X₁—Х₂ осталось ровно 500 литров. Заправляемся послед­ними 500 литрами и едем в точку 500—X₁, израсходовав на это Х₂ литров.

Теперь мы находимся в точке 500— X₁, затратив на проезд 5Х₂ литров топлива. Здесь оставлено в общей сложности 1500—5Х₂ литров. Это количество должно быть равно 1000 литрам, т. е. Х₂==500/5. Из этого заключаем, что 1500 литров позволяют нам пролететь

D = 500 + X₁+Õ₂ = 500 (l+1/3+1/5) километров.

Продолжая индуктивно процесс отрабатывания назад, получаем, что n баков горючего позволяют нам пролететь Dn километров, где

D =500 (1+1/3+1/5+...+1/(2n-1)).

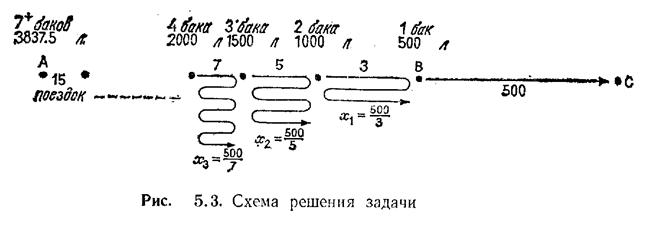
Нужно найти наименьшее значение п, при котором Dn = 1000. Простые вычисления показывают, что для n=7 имеем D₇=977,5 километра, т. е. семь баков, или 3500 литров, топлива дадут нам возможность пролететь 977,5 мили. Полный восьмой бак — это было бы уже больше, чем нам надо, чтобы перевезти 3500 литров из точки А в точку, отстоящую на 22,5 мили (1000—977,5) от А. Читателю представляется самостоятельно убедиться в том, что для доставки 3500 литров топ­лива к отметке 22,5 мили достаточно 337,5 литра. Таким образом, для того чтобы пересечь на вертолете пустыню из А в С, нужно 3837,5 литра горючего.

Теперь алгоритм транспортировки горючего может быть пред­ставлен следующим образом. Стартуем из А, имея 3837,5 литра. Здесь как раз достаточно топлива, чтобы постепенно перевезти 3500 литров к отметке 22,5 мили, где мы в конце концов окажемся с пустым баком и запасом горючего на семь полных заправок. Этого топлива достаточно, чтобы перевезти 3000 литров к точке, отстоящей на 22,5+500/13 километров от А, где бак машины будет опять пуст. После­дующие перевозки приведут нас к точке, отстоящей на 22,5+500/13+500/11 километров от А, с пустым баком машины и 2500 литрами.

Продолжая таким образом, мы продвигаемся вперед благодаря анализу, проведенному методом отрабатывания назад. Вскоре мы окажемся у отметки 500 (1—1/3) = 1000/3 километров с 1000 литрами топ­лива. Затем мы перевезем 500 литров в В, зальем их в бак вертолета и долетим без остановки до С. Рис.5.3 иллюстрирует весь этот процесс.

Для тех, кто знаком с бесконечными рядами, заметим, что Dn есть n-я частная сумма нечетного гармонического ряда. Поскольку этот ряд расходится, алгоритм дает возможность пересечь любую пустыню. Как можно модифицировать этот алгоритм для того, чтобы оставить достаточно горючего в различных точках пустыни для воз­вращения в А?

Возникает вопрос, можно ли пролететь 1000 километров, затратив меньше чем 3837,5 литра горючего. Оказывается, что нельзя. Доказатель­ство этого факта довольно сложно. Однако можно высказать следую­щий, довольно правдоподобный довод. Очевидно, мы действуем наилучшим образом для k=1. При k=2 мы используем наш план для k=1 и затем вводим в действие второй бак горючего для того, чтобы оказаться как можно дальше от В. Исходная предпосылка для k баков заключается в том, что мы знаем, как действовать наилучшим образом в случае с k—1 баками, и отодвигаемся как можно дальше назад с помощью k-ro бака.

5.2 Метод эвристики

Метод решения задачи на интуитивном уровне, правильность которого доказать не возможно, но тем не менее, который дает хорошее, но не обязательно оптимальное решение называют эвристический метод.

Или другими словами эвристический алгоритм, или эвристика, определяется как алго­ритм со следующими свойствами:

1. Он обычно находит хорошие, хотя не обязательно оптимальные решения.

2. Его можно быстрее и проще реализовать, чем любой известный точный алгоритм (т. е. тот, который гарантирует оптимальное решение).

Понятия «хороший» н «обычно» в свойстве 1 меняются от задачи к задаче.

Возникает вопрос почему решение многих задач основано на этом методе, который дает не обязательно оптимальное решение. Дело в том, что иногда оптимальное решение достичь не возможно, либо процесс достижения оптимального решения настолько трудоемок, что проще получить пусть не оптимальное, но достаточно хорошее решение за значительно меньшее время. Например, если для решения задачи все известные точные алгоритмы требуют нескольких лет машинного времени, то мы можем охотно принять любое нетривиальное приближенное решение, которое может быть получено за разумное время. С другой стороны, имея быстрое, близкое к оптимальному решение, мы можем стремиться все же к точному решению.

Хотя не существует универсальной структуры, которой можно описать эвристические алгоритмы, многие из них основываются или на методе частных целей, или на методе подъема.

Рассмотрим при каких случаях возникает эвристический алгоритм.

- когда решение задачи не достижимо, или очень трудоемко традиционными методами;

- когда не возможно доказать правильность используемого алгоритма

Итак, для первого случая общий подход к построению эвристических алгоритмов заключается в перечислении всех требований к точному решению и разделении требований на два класса, например:

1. Те, которые легко удовлетворить.

2. Те, которые не так легко удовлетворить.

Или

1. Те, которые должны быть удовлетворены.

2. Те, по отношению к которым мы могли бы пойти на компромисс.

Тогда цель построения алгоритма — создать алгоритм, гарантиру­ющий выполнение требований 1-го класса, но не обязательно 2-го. Это не означает, что для удовлетворения требований 2-го класса не делается никаких попыток, это просто означает, что не может быть дано никаких гарантий, что они будут удовлетворены.

По отношению ко второму случаю можно сказать, что часто очень хорошие алгоритмы должны рассматриваться как эвристические. Например, предположим, что мы построили быстрый алгоритм, который, кажется, работает на всех тестовых задачах, но мы не можем доказать, что алгоритм правильный. Пока не дано такое доказательство, алгоритм следует рассматривать как эвристику.

В качестве примера рассмотрим следующий «грубый» алгоритм решения задачи коммивояжера, рассмотренному нами в главе 3.