Решение задачи коммивояжера

1. Приведение матрицы стоимостей

1 2 3 4 5 1 2 3 4 5 Н

1 ¥ 25 40 31 27 1 ¥ 0 15 3 2 25

2 5 ¥ 17 30 25 2 0 ¥ 12 22 20 5

3 19 15 ¥ 6 1 3 18 14 ¥ 2 0 1

4 9 50 24 ¥ 6 4 3 44 18 ¥ 0 6

5 22 8 7 10 ¥ 5 15 1 0 0 ¥ 7

Н 0 0 0 3 0

Нс=47

2. Выбор ребра ветвления

Пути соответствующие значениям 0 следующие (1,2), (2,1), (3,5), (4,5), (5,3), (5,4)

Значения на которое предстоит увеличить суммарную Нс = 47 соответственно равны: 2+1=3; 12+3=15; 2+0=2; 3+0=3; 0+12=12; 0+2=2.

Привило по которому производится это вычисление, следующее:

(наименьшая стоимость в строке i, не включая Cij)+(наименьшая стоимость в столбце j, не включая Сij),

где Сij соответствует 0 значениям приведенной матрицы.

Выбирает ребро (2,1), как максимальный элемент из списка.

3. Исключение из матрицы стоимостей строки 2 и столбца 1 и ее приведение.

2 3 4 5 2 3 4 5 Н

1 ¥ 15 3 2 1 ¥ 13 1 0 2

3 14 ¥ 2 0 3 13 ¥ 2 0 0

4 44 18 ¥ 0 4 43 18 ¥ 0 0

5 1 0 0 ¥ 5 0 0 0 ¥ 0

Н 1 0 0 0

Нс=3

4. Определение нижних границ стоимостей вершин

Для множества включающего ребро (2,1) 47+3=50

Для множества не включающего ребро (2,1) 47+15=62

Рассмотрение проводим для варианта имеющего нижнюю границу 50

5. Определяем ребро ветвления для вершины с нижней границей 50

Пути соответствующие значениям 0 следующие (1,5), (3,5), (4,5), (5,2), (5,3), (5,4)

Значения на которое предстоит увеличить суммарную Нс = 47 соответственно равны: 1+0=1; 2+0=2; 18+0=18; 13+0=13; 13+0=13; 0+1=1.

Выбирает ребро (4,5), как максимальный элемент из списка.

6. Исключение из матрицы стоимостей строки 4 и столбца 5 и ее приведение.

2 3 4 2 3 4 Н

1 ¥ 13 1 1 ¥ 12 0 1

3 13 ¥ 2 3 11 ¥ 0 2

5 0 0 0 5 0 0 0 0

Н 1 0 0

Нс=3

7. Определение нижних границ стоимостей вершин

Для множества включающего ребро (4,5) 50+3=53

Для множества не включающего ребро (4,5) 50+18=68

Рассмотрение проводим для варианта имеющего нижнюю границу 53

8. Определяем ребро ветвления для вершины с нижней границей 53

Пути соответствующие значениям 0 следующие (1,4), (3,4), (5,2), (5,3).

Значения на которое предстоит увеличить суммарную Нс = 47 соответственно равны: 12+0=12; 11+0=11; 11+0=11; 12+0=12.

Выбирает ребро (1,4).

9. Исключение из матрицы стоимостей строки 1 и столбца 4 и ее приведение.

2 3 2 3 Н

3 11 ¥ 3 0 ¥ 11

5 ¥ 0 5 ¥ 0 0

Н 1 0

Нс=11

Примечание: путь (5,2) мы положили равным ¥, так как ребро (1,4), вместе с ребрами (2,1), и (4,5) образует путь и следовательно пути где участвуют точки 5 и 2 уже присутствуют в рассмотрении, следовательно путь (5,2) не осуществим по условию задачи.

7. Определение нижних границ стоимостей вершин

Для множества включающего ребро (1,4) 53+11=64

Для множества не включающего ребро (1,4) 53+12=65

8. Таким образом, у нас получился один из оптимальных вариантов со стоимостью 64. Ему соответствует общий путь (1,4) - (4,5) - (5,3) - (3,2) - (2,1). Ребра (2,1), (4,5) и (1,4) выбраны как ребра ветвления, а ребра (3,2) и (5,3) - остаются в матрице (п.9).

Естественно заметить, что одна из рассмотренных ранее нижних границ для вершины исключающий вариант с ребром (2,1) равна 62, поэтому теперь проводим решение для этой вершины и вычисляем нижние границы для нее. Решение провидится аналогично.

9. Исследование вершины исключающей путь (2,1)

9.1 Матрица для нее записывается также как в п.1 за исключением того, что значение (2,1) приравнивается бесконечности, так как путь (2,1) для этих вариантов не возможен.

1 2 3 4 5 1 2 3 4 5 Н

1 ¥ 25 40 31 27 1 ¥ 0 15 3 2 25

2 ¥ ¥ 17 30 25 2 ¥ ¥ 0 10 8 17

3 19 15 ¥ 6 1 3 15 14 ¥ 2 0 1

4 9 50 24 ¥ 6 4 0 44 18 ¥ 0 6

5 22 8 7 10 ¥ 5 12 1 0 0 ¥ 7

Н 3 0 0 3 0

Нс=62

9.2 Определяется ребро ветвления, это будет (4,1).

9.3. Для него определятся нижние границы. Это будет 74 исключающее ребро (4,1), и 62 включающее ребро (4,1).

9.4. Необходима еще одна итерация. Оставим это в качестве упражнения.

Весь проделанный ход рассуждения иллюстрирует схема представленная на рис. 5.12.

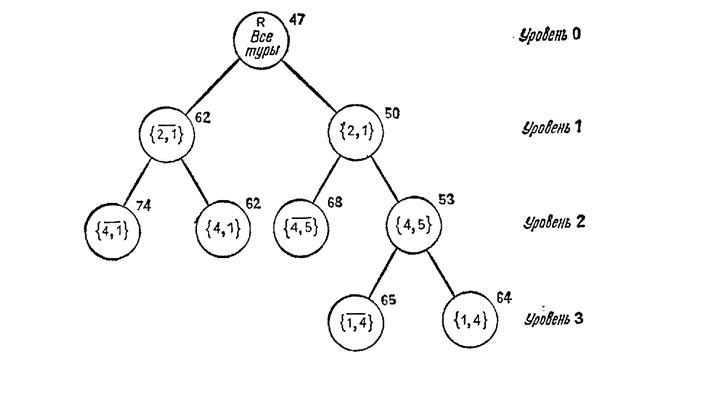
Рис. 5.12. Дерево поиска

Таким образом мы полностью рассмотрели алгоритм решения задачи - названный как метод ветвей и границ. И хотя, этот метод довольно сложен, эффективность его решение в ряде случае бесспорна. В отношении его сложности можно сказать, что существуют различные эвристические приемы, которые ускоряют этот сложный алгоритм и в ряде случаев еще и упрощают его.

5.5. Рекурсия

Рекурсивным называется объект, частично состоя­щий или определяемый с помощью самого себя. Ре­курсия встречается не только в математике, встре­чается она и в повседневной жизни. Кто не видел рекламной картинки, содержащей свое собственное изображение?

В частности, рекурсивные определения представ­ляют собой мощный аппарат в математике.

Примером рекурсии может является вычисление факториала Функция «факториал» n! (для неотрицательных целых чисел) рекурсивно определяется как

0! = 1

n! = n*(n—1)! Еслси n>0

Уравнение вида n! = n*(n-1)! называется рекуррентным соотношением. Рекуррентные соотношения выражают значения функции при помощи других значений, вычисленных для меньших аргументов.

Уравнение О!=1 — нерекурсивно определенное начальное значение функции. Для каждой рекурсивной функции нужно хотя бы одно такое начальное значение, в противном случае ее нельзя вычислить в явном виде,

Аналогично числа Фибоначчи определяются следующей беско­нечной последовательностью целых чисел: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,.... Проверка показывает, что N-н элемент этой последова­тельности равен сумме двух непосредственно предшествующих эле­ментов. Таким образом, значение FIB(N) для N-того числа может быть определено из рекуррентного соотношения:

FIB(N)=FIB(N—1)+FIB(N—2).

Так как FIB(N) определено через два разных значения для мень­ших аргументов, необходимы два начальных значения. Ими служат

FIB(1)=1, FIB(2)=1.

Определенные здесь числа Фибоначчи являются рекурсивным решением следующей задачи:

Каждый месяц самка из пары кроликов приносит двух кроликов (самца и самку). Через два месяца новая самка сама приносит пару кроликов. Нужно найти число кроликов в конце года, если в начале года была одна новорожденная пара кроликов и в течение этого года кролики не умирали,

Эта последовательность названа в честь итальянского математика Фибоначчи, который в 1202 г, сформулировал изложенную здесь задачу.

Функция Аккермана

Две рекурсивные функции, рассмотренные до сих пор, были до­статочно простыми. Поэтому, чтобы не сложилось неправильное впе­чатление о том, насколько сложны рекурсивные функции, представим следующую, довольно простую на первый взгляд, дважды рекурсив­ную функцию, известную как функция Аккермана. Функция дважды рекурсивна, если сама функция и один из ее аргументов определены через самих себя.

N + 1, если М = 0;

А (М, N) = А (М—1, 1), если N = 0;

A [М—1, А (М, N—1)] в остальных случаях.

Беглый просмотр рис. 5.13 показывает, как трудно вычислить эту функцию даже для таких малых аргументов, как М = 4 и N=2. Заметьте, например, что А (4, 1)=A(3, 13).

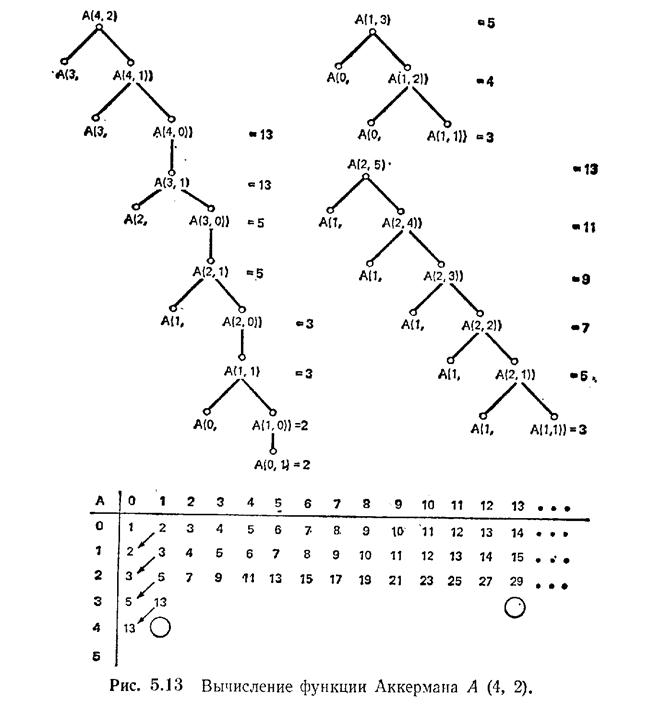
Рис.5.13 Вычисление функции Анкермана А(4,2)

Мощность рекурсивного определения заключается, очевидно, в том, что оно позволяет с помощью ко­нечного высказывания определить бесконечное мно­жество объектов. Аналогично с помощью конечной рекурсивной программы можно описать бесконечное вычисление, причем программа не будет содержать явных повторений. Однако рекурсивные алгоритмы лучше всего использовать, если в решаемой задаче, вычисляемой функции или структуре обрабатывае­мых данных рекурсия уже присутствует явно. В об­щем виде рекурсивную программу Р можно выра­зить как некоторую композицию Р из множества опе­раторов S (не содержащих Р) и самой программы Р:

P = P[S,P]

Для выражения рекурсивных программ необходимо и достаточно иметь понятие процедуры или подпро­граммы, поскольку они позволяют дать любому опе­ратору имя, с помощью которого к нему можно обращаться. Если некоторая процедура Р содержит явную ссылку на саму себя, то ее называют прямо рекурсивной, если же Р ссылается на другую про­цедуру Q, содержащую (прямую и косвенную) ссыл­ку на Р, то Р называют косвенно рекурсивной. По­этому по тексту программы рекурсивность не всегда явно определима.

Как правило, с процедурой связывают множество локальных объектов, т. е. множество переменных, констант, типов и процедур, которые определены - только в этой процедуре и вне ее, не существуют или не имеют смысла. При каждой рекурсивной актива­ции такой процедуры порождается новое множество локальных, связанных переменных. Хотя они имеют те же самые имена, что и соответствующие элементы локального множества предыдущего «поколения» этой процедуры, их значения отличны от последних, а любые конфликты по именам разрешаются с по­мощью правил, определяющих область действия идентификаторов; идентификатор всегда относится к самому последнему порожденному множеству пере­менных. Это же правило справедливо и для пара­метров процедуры, по определению связанных с са­мой процедурой.

Подобно операторам цикла, рекурсивные проце­дуры могут приводить к незаканчивающимся вычис­лениям, и поэтому на эту проблему следует особо обратить внимание. Очевидно основное требование, чтобы рекурсивное обращение к Р управлялось не­которым условием В, которое в какой-то момент ста­новится ложным. Поэтому более точно схему рекур­сивных алгоритмов можно представить в любой из следующих форм;

P º IF В THEN P(S,P) END

или

P ºP (S, IF В THEN P END)

В практических приложениях важно убедиться, что максимальная глубина рекурсий не только конечна, но и достаточно мала. Дело в том, что каждая рекурсивная активация процедуры Р требует памяти для размещения ее переменных. Кроме этих локаль­ных переменных нужно еще сохранять текущее «со­стояние вычислений», чтобы можно было вернуться в него по окончании новой активации Р.

Если взять такой язык как Турбо-Бейсик, то рекурсивными являются подпрограммы: процедура SUB и FUNCTION.

В рекурсивных процедурах реализован принцип "разделяй и властвуй" - сложные алгоритмы разделяются на более простые и решаются. Ниже приведен текст программы для поиска и возврата длины строки.

DECLARE FUNCTION St% (x$)

INPUT "введите строку", in$

PRINT "Длина строки равна", St%(in$)

INPUT a

FUNCTION St% (x$)

IF x$ = "" THEN

REM длина нулевой строки равна 0

St% = 0

ELSE

REM ненулевая строка - рекурсия

REM длина ненулевой строки равна 1 + длина оставшийся части строки.

St% = 1 + St%(MID$(x$, 2))

END IF

END FUNCTION

Рекурсивные алгоритмы особенно подходят для задач, где обрабатываемые данные определяются в терминах рекурсии. Однако это не означает, что та­кое рекурсивное определение данных гарантирует бесспорность употребления для решения задачи ре­курсивного алгоритма. Фактически объяснение кон­цепций рекурсивных алгоритмов на неподходящих для этого примерах и вызвало широко распространен­ное предубеждение против использования рекурсий в программировании; их даже сделали синонимом не­эффективности.

Программы, в которых следует избегать алгорит­мической рекурсии, можно охарактеризовать некото­рой схемой, отражающей их строение. Это следующие схемы:

PºIF В THEN S; Р END

PºS; IF В THEN Р END

Специфично, что в них есть единственное обращение к Р в конце (или начале) всей конструкции.

Такие задачи могут быть решены с помощью простой итерации. Итерация - это последовательное приближение к намеченной цели, когда вычисление нового значения осуществляется циклически, через значения определенные на предыдущем шаге.

Например, вычисление факториала некоторого числа может быть реализовано через рекурсивное решение. Ниже приводится пример такой программы.

DECLARE SUB S (m, f)

INPUT "Введите число", m

m1 = m

CALL S(m, f)

PRINT "Число и его факториал", m1, f

SUB S (m, f)

PRINT f

IF f = 0 THEN f = m

IF m > 1 THEN m = m - 1: f = f * m: CALL S(m, f)

END SUB

Ниже приведен текст программы, когда вычисление факториала можно провести используя итерацию.

INPUT "Введите число", m

m1 = m

IF f = 0 THEN f = m

WHILE m > 1

m = m - 1: f = f * m

WEND

PRINT "Число и его факториал", m1, f

Как видно из примеров, решение задачи для данного случая построенное методом простой итерации более просто и следовательно, более предпочтительнее.

В общем-то программы, построенные по схемам

PºIF В THEN S; Р END

PºS; IF В THEN Р END

нужно переписывать в программы построенные по схемам

Рº(X=Xo; WHILE B S WEND)

Итак, урок таков: следует избегать рекурсий там, где есть очевидное итерационное решение. Однако это не означает, что от рекурсий надо отказываться вообще. Существует много хороших примеров применения рекурсии.

Общий вывод этого раздела состоит в том, что решение задачи может быть проведено как рекурсивно, так и с помощью итераций. А конкретное решение задачи (рекурсия или итерация) зависит прежде всего от построенного алгоритма.

5.6. Моделирование

Большая часть алгоритмов, которые мы рассматривали до сих пор решает относительно простые задачи. Многие из этих задач легко сформулировать и смоделировать. Они содержат не много параметров, и обычно их можно решить аналитически. Более того получающиеся алгоритмы довольно компактны.

Эти задачи резко отличаются от задач, описывающих большие системы, или системы имеющих многовариантную сложность, например военные расчеты, космические полеты, прогнозирование климата, управление производством и принятия административных решений.

Задачи относящиеся к большим системам очень трудно моделировать, анализировать и решать. Например, трудно определить все переменные, влияющие на поведение системы, внутренние связи между переменными.

Появление ЭВМ позволило подойти к изучению таких сложных систем при помощи моделирования. Машинное моделирование - это процесс экспериментирования на ЭВМ над моделью динамической системы. Непосредственная цель этих экспериментов — наблюдение за поведением системы при заданных предположениях, условиях и значениях параметров. Конечной целью может быть:

формулиро­вание стратегии управления,

определение оптимальных или воз­можных конфигураций системы;

установление реальных произ­водственных планов или решение вопроса об оптимальных эконо­мических стратегиях;

и многое другое.

Преимущества машинного моделирования многочисленны. Они позволяют изучить с желаемой степенью детальности все части си­стемы, объединенные в единое целое, в то время как аналитически можно изучить только отдельные части системы. Всеми переменными можно управлять, и все можно измерять. Машинное моделирование позволяет получить информацию о реальной системе, когда непрак­тично проводить на ней прямой эксперимент. Имитация позволяет испытать систему до того, как на соответствующую реальную систему затрачены время и деньги,

Имитационные эксперименты можно проводить в разных масшта­бах времени. Время может быть замедлено, чтобы проверить на мик­роскопическом уровне свойства, которые трудно проанализировать в реальной системе. Время может быть ускорено, чтобы охватить все на макроскопическом уровне, например, при изучении отдаленных последствий тех или иных допущений. Время также можно остано­вить, повернуть вспять и проиграть заново, чтобы изучить случаи необычного поведения более детально. В реальных системах часто бывает, что, начав некоторый эксперимент, остановить его нельзя.

Кто-то вполне может задать вопрос: почему мы не прибегаем к моделированию во всех случаях? Существует несколько частичных ответов на этот вопрос. Во-первых, моделирование — это эксперимен­тальный метод. Поэтому всегда возникает серьезный вопрос, как ис­толковать результаты. Важно понять, что достоверность выходных данных зависит от того, в какой степени модель и основные допуще­ния отражают характеристики системы. Во-вторых машинная имитация может стать дорогостоящей, если модель становится чрезмерно детализи­рованной.

Область имитационного моделирования слишком обширна, чтобы всесторонне охватить ее здесь. Для наших целей достаточно будет представить несколько важных соображений, относящихся к построе­нию имитационных моделей.

1. Для моделирования процессов необходимо разработать физическую модель процессов, которая отражает реальную картину событий. При этом необходимо сделать некоторые допущения, которые не затрагивают существа исследуемого явления, но в тоже время позволяют значительно упростить задачу.

Для процессов моделирования - это пожалуй один из главных вопросов - определение факторов влияющих на событие и установление их влияние между собой.

2. В зависимости от того на что направлены исследования устанавливается метод планирования событий. Он зависит только от рассматриваемого явления и определяется только им. Планирование событий может носить детерминированный или случайный характер. Например, детерминированный характер будут носить модели расчета поведения аппаратуры при ядерном взрыве, а случайный характер - модели обслуживания случайных событий, выход из строя каких-то устройств и т.п.

Причем модель будет работать таким образом, что изменение ее характеристик будет наблюдаться при наступлении какого-либо события, т.е. нет нужды в беспрерывном ходе часов когда ничего не случается.

3. Результаты моделирования должны отражать реальную ситуацию.

Вообще говоря, это очень важная и обширная тема и ее рассмотрение возможно применительно для решения какой-либо задачи.

Глава 6. Алгоритмы машинной математики больших массивов данных.

В предыдущих разделах нами были рассмотрены основные принципы разработки алгоритма решения задачи. В настоящем разделе нами будут рассмотрены методы машинной математики для обработки больших данных. Как известно, с данными необходимо проводить такие операции многочисленные операции, но доминирующую роль играют такие операции, как сортировка и поиск. Рассмотрим их наиболее подробно.

6.1. Сортировка

Сортировку следует понимать как процесс перегруппировки заданного множества объектов в некотором определенном порядке. Цель сортировки - облегчить последующий поиск элементов в таком отсортированном множестве. Эта почти универсальная, фундаментальная деятельность. Мы встречаемся с отсортированными данными везде: в оглавлениях книг, в словарях, библиотеках и т.п. Даже "малышей" учат держать свои вещи "в порядке", и они уже сталкиваются с азами сортировки.

Сортировка стала важным предметом вычислительной математики в основном потому, что она отнимает значительную часть времени работы ЭВМ. Осознание того, что 25% всего времени вычислений рас­ходуется на сортировку данных, придает особое значение эффективным алгоритмам сортировки.

К сожалению, нет алгоритма сортировки, который был бы наилуч­шим в любом случае. Трудно даже решить, какой алгоритм будет лучшим в данной ситуации, так как эффективность алгоритма сор­тировки может зависеть от множества факторов, например от того, (1) каково число сортируемых элементов; (2) все ли элементы могут быть помещены в доступную оперативную память; (3) до какой степени элементы уже отсортированы; (4) каковы диапазон и распределение значений сортируемых элементов; (5) записаны ли элементы на диске или магнитной ленте; (6) каковы длина, сложность и требования к памяти алгоритма сортировки; (7) предполагается ли, что элементы будут периодически исключаться или добавляться; (8) можно ли элементы сравнивать параллельно.

Очевидно, что с отсортированными данными работать легче, чем с произвольно расположенными. Когда элементы отсортированы, их проще найти (как в телефонном справочнике), обновить, исключить, включить и слить воедино. На отсортированных данных легче опреде­лить, имеются ли пропущенные элементы (как в колоде игральных карт), и удостовериться, что все элементы были проверены. Легче также найти общие элементы двух множеств, если они оба отсортированы. Сортировка применяется при трансляции программ, когда состав­ляются таблицы символов; она также является важным средством для ускорения работы практически любого алгоритма, в котором часто нужно обращаться к определенным элементам.

Обычно сортируемые элементы представляют собой записи данных определенного вида. Каждая запись имеет поле ключа и поле инфор­мации. Поле ключа содержит положительное число, обычно целое, и записи упорядочиваются по значению ключа. Однако учитывая, что в данном разделе, важно понять сам метод сортировки, мы не будем делать существенного различия между ключом элемента массива, и самим элементом массива, считая в качестве элемента массива простое положительное число.

Выбор алгоритма зависит от структуры обрабатываемых данных - это почти закон, но в случае сортировки такая зависимость столь глубока, что соответствующие ей методы были разбиты на два класса - сортировку массивов и сортировку файлов (или последовательностей). Иногда их называют внутренней и внешней сортировкой, поскольку массивы хранятся в оперативной памяти со случайным доступом, а файла размещаются во внешней памяти. Уже на примере сортировке карточек становится очевидным существенное различие в этих подходах. Если карты "выстороены" в виде массива, то они как бы лежат на столе, и сортирующий видит их сразу все. Если карты образуют файл, то это предполагает, что видна только верхняя карта в каждой из стопок. Такое ограничение накладывает существенное отличие в методах сортировок.

В этом разделе мы рассматриваем два метода сортировки массивов: сортировка простыми включениями и так называемый метод быстрой сортировки. Кроме того рассмотрим принципы сортировки пузырьками и сортировка методом отыскания наименьшего (наибольшего) ключа.

Рассмотрение сортировок последовательностей изложено на основе метода в котором используется сортировка с помощью слияния.

6.2. Сортировка массивов

Методы сортировки массивов можно условно разбить на две группы:

- сортировка когда элементы массива а передаются в результирующий массив b;

- сортировка когда элементы массива а перегруппируются в самом массиве а, который и будет результирующий.

Выбор методов сортировки зависит от условий задачи, и хотя в ряде случаев предпочтительнее выглядят методы второй группы, так как они экономят память, нередко в условиях сортировки требуется помимо отсортированного списка сохранять неотсортированный.

Рассмотрим эти методы.