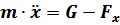 ,
,
где 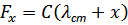 ,
,
тогда
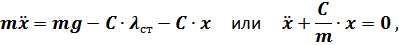
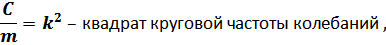
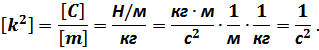
В итоге 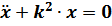 .
.
Решение этого дифференциального уравнения – закон колебаний
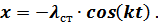
График незатухающих свободных колебаний (рис. 4)
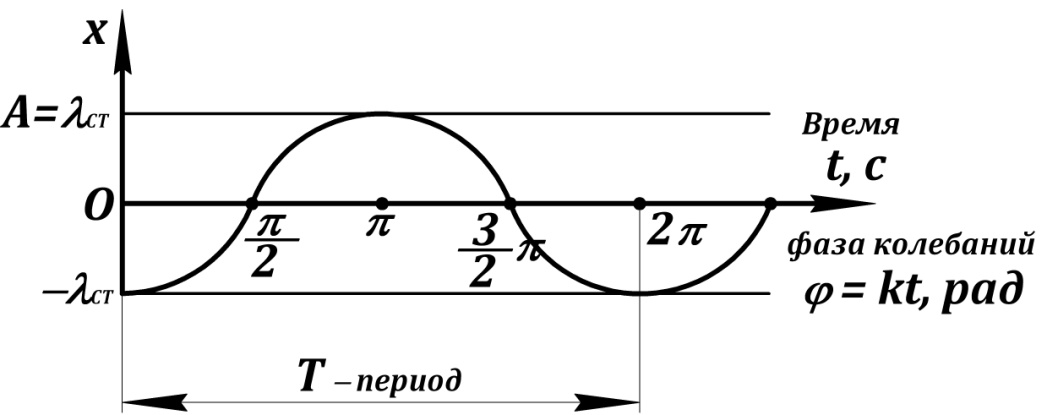
Рис. 4. График незатухающих свободных колебаний материальной точки
Расчётные формулы
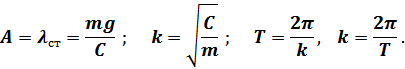
С УЧЁТОМ СОПРОТИВЛЕНИЯ (ЗАТУХАЮЩИЕ)
Пример: колебания на пружине тела, погруженного в воду, тело – цилиндр вдвое легче воды (радиус – 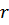 , удельный вес –
, удельный вес – 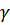 ).
).
От положения равновесия тело погружено в воду на величину 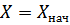 .
.
К восстанавливающей силе пружины
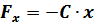
добавляется выталкивающая сила Архимеда
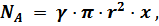
а при колебаниях возникает сила вязкого сопротивления
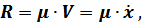
где 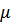 – коэффициент пропорциональности силы
– коэффициент пропорциональности силы 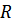 скорости
скорости 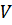 ,
,
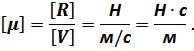
 2015-05-06
2015-05-06 987
987








