2015-05-06
1438
Как известно, в электротехнике мощность P и энергия E определяются выражениями
,
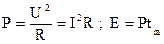где U - напряжение; I - ток; R - сопротивление; tm - время наблюдения. Эти энергетические характеристики пропорциональны квадрату напряжения или тока.
Пусть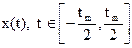 
есть напряжение (или ток) на сопротивлении R = 1 Ом. Тогда при описании сигнала во временной области мгновенная мощность, средняя мощность и энергия будут равны:
,
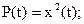
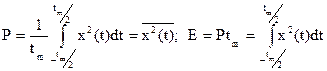где обозначение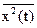 
означает усреднение по времени квадрата сигнала.
Если допустить периодическое продолжение сигнала x(t) с периодом T=tm, то среднюю мощность можно находить, исходя из спектрального представления периодического сигнала в частотной области:
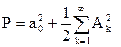- для ряда (2.4.1);
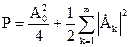- для ряда (2.4.2);
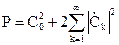- для ряда (2.4.4).
Часто сигнал задается на бесконечном интервале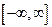 
. Тогда
.
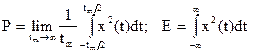Здесь различают два вида сигналов:
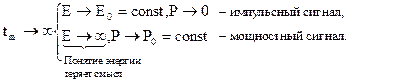
Пусть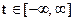 
и энергетический сигнал 
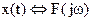. Выразим энергию сигнала через его частотную характеристику. Для этого в выражении x2(t) одну из функций представим в виде обратного преобразования Фурье. Тогда энергия сигнала
.
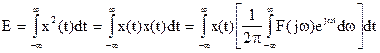Изменим порядок интегрирования. Тогда
.
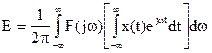Внутренний интеграл в квадратных скобках имеет вид
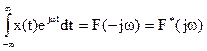- комплексно-сопряженная функция.
Так как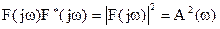 
, где A(w) - амплитудный спектр, то окончательно получим
.
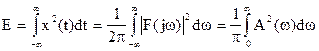Это соотношение называется равенством Парсеваля (или теоремой Рейли).
Величина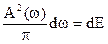 
- это доля энергии сигнала, приходящаяся на полосу частот 
.
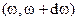Функция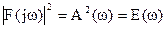 
называется спектральной плотностью энергии или энергетическим спектром. Она является четной функцией и определяет величину энергии, приходящейся на полосу в 1 рад/с.
Для мощностных сигналов рассматривают среднюю мощность, так как понятие энергии теряет смысл. Пусть функция x(t) задана на конечном интервале tm и имеет спектральную функцию
.
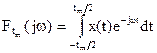Тогда энергия сигнала конечна и равна
.
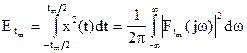Средняя мощность при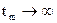 
будет
,
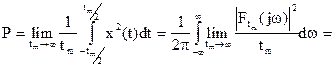
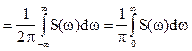где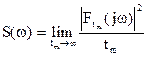 
- спектральная плотность мощности.
Спектр плотности мощности сигнала сохраняет информацию только об амплитудах спектральных составляющих. Информация о фазе теряется. Поэтому все сигналы с одинаковым спектром амплитуд и различными спектрами фаз будут иметь одинаковые спектры плотности мощности.
Данному сигналу соответствует единственный спектр плотности мощности. Обратное утверждение неверно: один и тот же спектр плотности мощности соответствует большому числу сигналов.
