Выделение гармонического сигнала из шума, когда его период известен

Рассмотрим теперь случай, когда период полезного сигнала известен, но неизвестна его «фаза», да и само наличие под вопросом. В этом варианте целесообразно использовать алгоритм вычисления взаимокорреляционной функции аддитивной смеси полезного сигнала и шума и опорным сигналом, период которого равен периоду полезного сигнала. Возможный выигрыш в отношении сигнал/шум рассмотрим на примере гармонического сигнала. Опорный сигнал 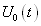тоже положим гармоническим, но с другой амплитудой и фазой 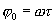. Шум 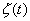будем считать «белым».

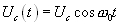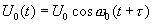; (16.7)

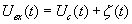
Таким образом искомая взаимокорреляционная функция будет

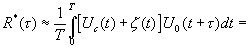
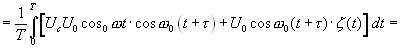
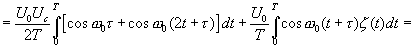
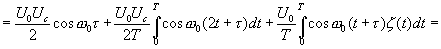
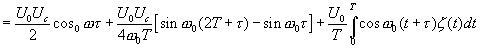(16.8)

Второй член в (4.8) можно рассматривать, как фон при конечном времени интегрирования, тогда, как третий интеграл имеет смысл «шума».

И «фон» и «шум» убывают при увеличении времени интегрирования Т. Очевидно, что «фон» убывает как 1/Т. Характер убывания «шума» при увеличении Т рассмотрим более подробно, отдельно.

Для оценки величины «шума» используем соотношение Хинчина:

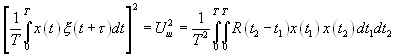(16.9).

Здесь 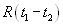— корреляционная функция случайного процесса, x(t) - детерминированная функция. Примем условия рассмотренного выше примера: шум на входе будем полагать «белым» со спектральной плотностью мощности 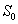, на входе корреляционного фильтра включен RC фильтр с коэффициентом передачи.

.

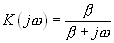Выше было показано, что корреляционная функция случайного процесса на выходе такого RC фильтре имеет вид:

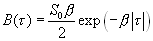(16.3)

Подставляя эти функции в (16.9) и вычисляя двойной интеграл, получаем громоздкое выражение (см.приложение), включающее члены, имеющие различное убывание при увеличении интервала интегрирования Т.

Если учесть только наиболее медленно убывающий член 1/T, то приближенно получаем:

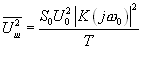(16.10).

Эта формула и описывает мощность «шума» на выходе корреляционного фильтра, обусловленного конечным временем интегрирования Т. «Амплитуда шума» соответственно:

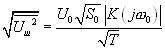(16.11).

Заметим, что роль частотного интервала здесь играет величина 1/T Величина же 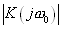просто безрамерный коэффициент.

Обращаясь к (4.8), напомним, что первый член описывает взаимокорреляционную функцию детерминированных сигналов, полезного 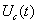и опорного 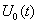и, следовательно, имеет смысл полезного сигнала на выходе корреляционного фильтра:

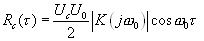(16.12).

Очевидно, что отношение сигнал/шум, (предполагая, что 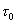выбирается так,чтобы 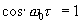), будет:

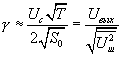(16.13).

Это важный результат: при накоплении периодического сигнала, которое можно вести на протяжении ряда периодов, отношение амплитуд сигнал/шум на выходе корреляционного фильтра увеличивается пропорционально корню квадратному от времени интегрирования. (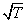). Понятно, что полученная зависимость сигнал/шум от времени интегрирования (как 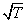) сохранится и в случае сложного периодического (импульсного) сигнала. Заметим, что в этом случае и опорный сигнал должен иметь спектр такой же, как и спектр полезного сигнала.

Реализовать описанный алгоритм возможно используя преобразование суммарного входного сигнала в цифровую форму, что позволит далее производить все операции вычисления 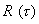с помощью программ на ЭВМ. При необходимости иметь выходной сигнал в аналоговой форме нужно использовать цифроаналоговый преобразователь. Кроме того, для ограничения спектра шума по входу необходимо сохранить, аналоговый фильтр, подобный рассмотренному в данном примере .

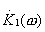В заключение этого раздела отметим, что результат здесь был получен на «временном языке», т. е. отношение сигнал/шум на выходе корреляционного фильтра, выражено как функция времени накопления (интегрирования). Но при этом пока неочевидно каков будет коэффициент передачи корреляционного фильтра в частотной области.

Ответ на этот вопрос удобно получить, рассмотрев аналоговый вариант корреляционного фильтра.

16.3. Аналоговый вариант корреляционного фильтра.

В радиотехнических терминах такой корреляционный фильтр реализуется схемой фазового детектора. Действительно, функционально схема фазового детектора реализует алгоритм определения взаимной корреляционной функции.

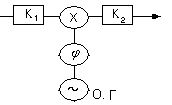
Рис. 16.1.

Эта схема содержит входной фильтр 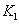, генератор опорного сигнала, перемножитель входного сигнала с опорным и накопитель- инерционный узкополосный фильтр 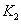, выполняющий приближенно операцию интегрирования.

Рассмотрим функционирование этой схемы, обращая внимание на преобразование спектра принимаемого (входного) сигнала.

Полезный сигнал опять будем считать гармоническим, а входной сигнал аддитивной смесью этого сигнала с «белым» шумом .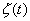

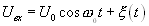
Пусть 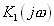есть резонансный RLC фильтр

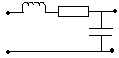
Рис.12

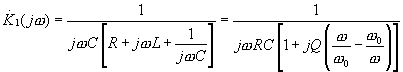(16.14)

будем считать 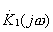узкополосным, тогда при выполнении условия 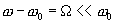получим приближенное выражение:

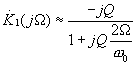, (16.15)

Удобно ввести ширину полосы пропускания фильтра 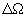при заданной неравномерности 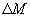, примем 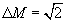. Тогда 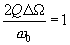, 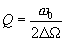-добротность, следовательно,

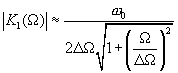(16.16)

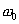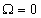Заметим, что на резонансной частоте имеем и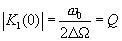

Будем далее учитывать нормированный модуль коэффициента передачи входного фильтра

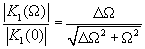(16.17)

Рассмотрим прохождение белого шума через такой резонансный фильтр 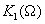, считая, что его спектральная плотность мощности- .

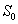Используя (2.3), имеем выражение для спектральной плотности мощности шума на выходе резонансного фильтра 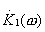, на входе перемножителя.

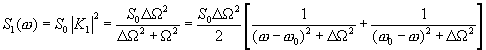(16.18)

В качестве второго сомножителя на перемножитель подается гармонический сигнал. Здесь возможны два варианта: первый — частота опорного сигнала равна частоте полезного сигнала (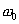). В этом случае фильтр 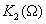должен быть фильтром НЧ. Полезный выходной сигнал будет представлен постоянной составляющей. Второй вариант- частота опорного сигнала 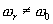. Здесь выходной фильтр 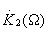должен быть резонансным на частоте .

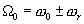Рассмотрим первый вариант: 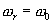, опорный гармонический сигнал

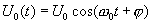(16.19)

Его спектр

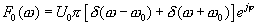(16.20)

Убедимся, что спектр (4.20) связан преобразованием Фурье с (16.19)

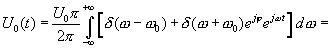
(16.21)

Здесь использовано известное свойство d (x) функции: .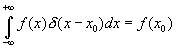

Итак, имеем спектры сомножителей, хотим найти спектр произведения — спектр на входе перемножителя. Используем формулу свертки в частотной области:

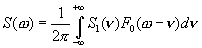(4.22)

Спектры сомножителей (4.19) и (4.20) изображены на рис.16.2.

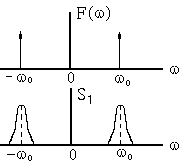
рис.16.2.

Подставив значения спектральных функций (16.18) и (16.20) в (16.22), получим спектральную плотность мощности шума на выходе перемножителя:

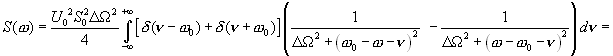
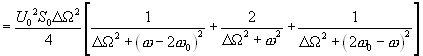(16.23)

Наконец, спектральная плотность мощности шума на выходе узкополосного НЧ фильтра 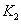будет содержать только полосу спектра вблизи 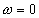. Это дает:

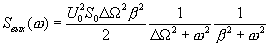(16.24)

Теперь легко найти мощность шума, имеющую такой спектр. Это удобно сделать так:

найти автокорреляционную функцию, соответствующую этому спектру и устремить t -> 0

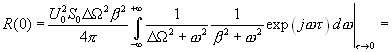
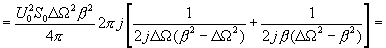
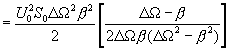(16.25)

Полоса фильтра 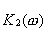выбирается много меньше, чем у фильтра 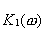, то есть 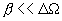, при этом (4.25) приблизительно дает:

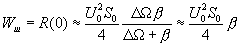(16.26)

Таким образом, мощность шума на выходе фазового детектора -корреляционного фильтра пропорциональна узкой полосе выходного фильтра 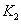равной DW 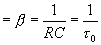Аналогично оценим величину и мощность полезного сигнала. Функция взаимной корреляции полезного гармонического сигнала была определена ранее (4.8),(4.12). Она описывает величину выходного полезного сигнала, в данном случае величину постоянной составляющей как функции задержки опорного сигнала .

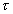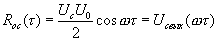(16.12)

Максимум сигнала на выходе фазового детектора получается при значениях

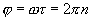
где n- целое число. Следует обратить внимание, что формула (16.12) описывает не мощность сигнала 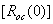, а его величину («амплитуду»). Множителю 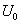следует придать смысл коэффициента усиления. Этот множитель присутствует и в выражении, оценивающем мощность шума. (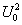). Поэтому мощность сигнала (его максимального значения при 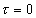) будет описываться так

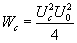(16.27)

А отношение сигнал/шум по мощности (см 16.26) есть:

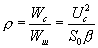(16.28)

соответственно, отношения сигнал/шум по амплитуде на выходе корреляционного фильтра — фазового детектора будет (16.29)