Периодическая последовательность прямоугольных импульсов

В качестве первого примера рассмотрим выделение полезного сигнала 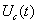, представляющего периодическую последовательность прямоугольных импульсов, которая принимается на фоне шума .

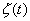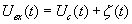
В роли приемного устройства, обеспечивающего желаемый выигрыш в отношении сигнал/шум, будем использовать корреляционный аналоговый фильтр, описанный выше. В качестве опорного сигнала будет использоваться аналогичная периодическая последовательность прямоугольных импульсов с той же частотой повторения, но, возможно другой длительности. Работу перемножителя в данном случае можно представлять как действие ключа: во время опорного импульса ключ замкнут, в его отсутствии — разомкнут. Коэффициент передачи перемножающего устройства периодически изменяется от единицы до нуля.

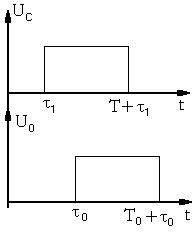
Рис 16.4.

Для нахождения 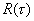, как и ранее, используем соотношение Фурье (16.1), найдя сначала соответствующую спектральную функцию 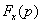. Для этого можно вначале определить спектр произведения одиночных импульсов, а затем, используя известную связь спектра одиночного и периодического сигналов, найти искомый спектр произведения периодических сигналов.

Принятые обозначения параметров импульсов изображены на рисунке

Изображения этих одиночных импульсов будут соответственно

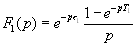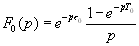, (16.31)

Изображение произведения временных функций определим, используя формулу свертки в частной области

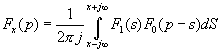(16.32)

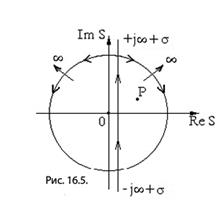
Заметим, что при интегрировании (16.32) точку Х на вещественной оси и комплексную точку Р следует взять настолько далеко вправо, чтобы для точки S, перемещающейся по прямой интегрирования (от 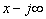до 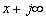) соблюдались два условия: во-первых, чтобы S оставалось в полуплоскости сходимости изображения 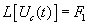, и во-вторых, чтобы P-S оставалось в полуплоскости изображения 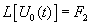[ Дёч ]

Подставляя (4.31) в (4.32) получаем, что необходимо вычислить четыре интеграла

,

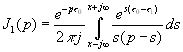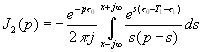
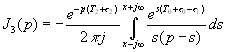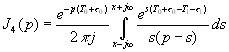, (16.33)

Значения этих интегралов зависят от знака показателя экспоненты. Покажем, как он влияет на примере вычисления 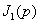, используя формулу разложения [ ], [ ], т. е. считая его по вычетам. Знаменатель в (16.33) имеет два корня S=0 и S=P, второй корень следует считать расположенным правее исходного контура интегрирования, (в правой полуплоскости S). При 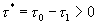, в соответствии с леммой Жордана, можем исходный контур замкнуть полуокружностью бесконечно большого радиуса в левой полуплоскости S. При этом в образовавшемся замкнутом контуре 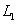окажется только полюс в точке S=0. Что дает:

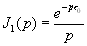
Если же 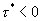, то лемма Жордана позволяет замкнуть исходный контур полуокружностью в правой полуплоскости S, теперь в замкнутом контуре окажется полюс S=P. Вычисляя этот вычет (с учетом знака (-) из-за изменения направления обхода по замкнутому контуру L), получаем:

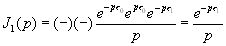
Аналогично вычисляются и остальные интегралы (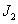, 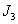и ).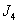

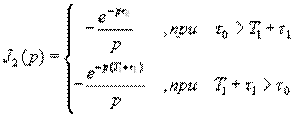
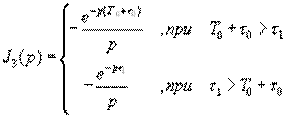
Результаты вычисления представлены в таблице 1.

Таблица 16.1	(4.34)

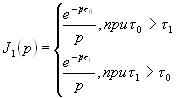
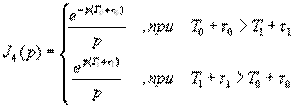
Очевидно, что искомое изображение 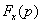(16.32) на выходе перемножителя-ключа получается суммированием 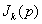с учетом взаимного положения 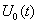и 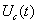во времени. Наглядно этот результат представлен на рисунке (в случаях B,C,D,E не выписаны сокращающиеся слагаемые).

Приведенные данные позволяют построить и функцию взаимной корреляции на выходе узкополосного, интегрирующего звена 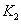, выделяющего (в данном примере) постоянную составляющую, величина которой зависит от взаимного положения импульсов во времени. Учитывая, что при изменении сдвига-задержки 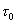опорного сигнала на входе звена 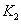меняется длительность импульса 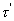и учитывая, что постоянная составляющая в спектре пропорциональна 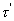, имеем:

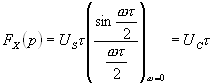(16.35)

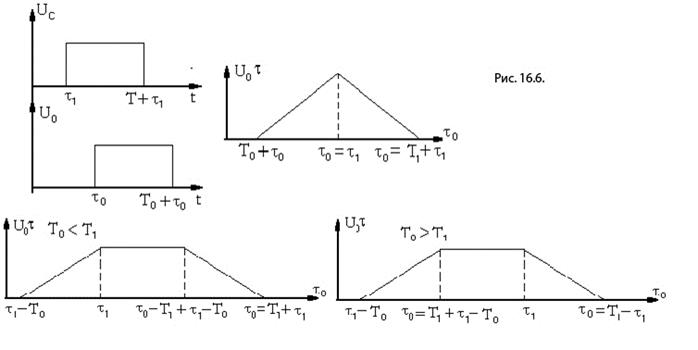
Получаем, что при изменении временного положения опорного импульса относительно сигнала 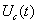взаимокорреляционная функция 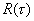будет иметь вид или трапеции (при 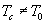), или видтреугольника (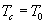) (см. рис.16.6). Теперь перейдем к анализу процессов в описанном фильтре при приеме периодической последовательн

ости импульсов. Проведем рассмотрение со спектральной точки зрения. Используем известную связь между спектральной плотностью 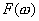одиночного импульса и дискретным спектром периодической последовательности таких импульсов, который описывается рядом Фурье. Связь такова:

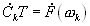и 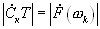(16.36),

где 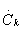— комплексная амплитуда катой гармоники спектра периодической последовательности, T- период следования импульсов, .

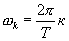Из формулы следует, что амплитуды гармоник периодической последовательности, умноженные на период Т, равны значениям функции модуля спектра одиночного импульса на частотах .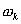

Для обеспечения оптимального приема периодической последовательности используем опорный сигнал также представляющий периодическую последовательность импульсов с тем же периодом. Таким образом, спектр опорного сигнала будет также дискретным; его гармоники будут иметь те же частоты, что и гармоники спектра входного сигнала.

Каков же будет спектр на выходе умножителя?

Каждая гармоника спектра опорного сигнала в результате перемножения дает суммарную и разностную частоту со всеми гармониками спектра сигнала. Если далее включен фильтр НЧ (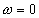) с полосой более узкой, чем дистанция между гармониками спектров (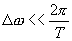), то будет выделена сумма постоянных составляющих, получающихся в результате перемножения гармоник спектров на совпадающих частотах. Все остальные комбинационные частоты не будут пропущены таким узкополосным фильтром. Следовательно, суммарный сигнал (как сумма постоянных составляющих) в результате перемножения и фильтрации одинаковых гармоник спектров входного и опорного сигналов будет

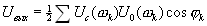(16.37),

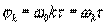
Сравнивая (16.37) с (16.14), видим, что данная сумма описывает взаимокорреляционную функцию периодических сигналов, имеющих одинаковые периоды Т.

Заметим, что данная взаимокорреляционная функция будет описывать периодическое повторение (по переменной t) полученной выше корреляционной функции для одиночных сигналов (16.34).

Какова же будет амплитудно-частотная характеристика такого фильтра?

В результате простого модельного эксперимента убеждаемся, что рассматриваемый фильтр будет иметь гребенчатую амплитудно-частотную (АЧХ) характеристику. Действительно, представим, что для определения АЧХ подаем на вход испытательный гармонический сигнал 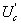с медленно изменяющейся во времени частотой. Так медленно изменяющейся, чтобы успевал устанавливаться переходной процесс в узкополосном усилителе. При этом обеспечим, что ширина полосы пропускания НЧ фильтра будет много меньше, чем частотный интервал между гармониками в спектре опорного периодического импульсного сигнала. Очевидно, что всякий раз, когда разность частоты какой либо гармоники спектра опорного сигнала и изменяющейся частоты испытательного сигнала оказывается в полосе пропускания НЧ фильтра, на его выходе появляется сигнал. Изменение амплитуды этого сигнала во времени приближенно описывает АЧХ этого низкочастотного фильтра. И так будет всякий раз при прохождении изменяющейся частоты испытательного сигнала 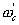по интервалам 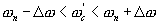, где 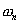- частоты гармоник спектра (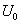) опорного сигнала. Таким образом, в целом полученная АЧХ будет иметь вид «гребенки». Максимумы зубцов этой гребенки будут лежать на частотах 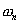, ширина же и форма каждого зубца определяются АЧХ узкополосного фильтра, интервалы между зубцами равны интервалам, между гармониками 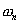опорного сигнала.