Связь интеграла Дюамеля с интегралом наложения

Подставив выражение для импульсной характеристики в интеграл наложения, получим

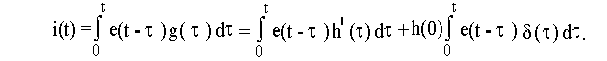
На основании фильтрующего свойства импульсной функции

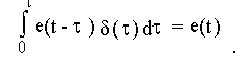
Тогда

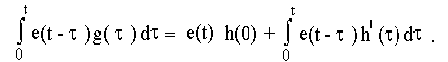
Таким образом

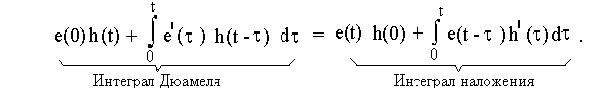
Пример 7. Для электрической цепи, приведенной в примере 1, рассчитать ток в индуктивной ветви с помощью импульсной характеристики при входном напряжении e(t) (рис.45).

Решение. Изображение отклика цепи на «дельта-функцию» является изображением импульсной характеристики

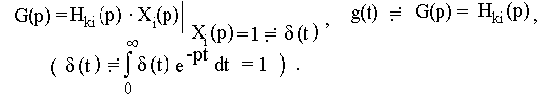
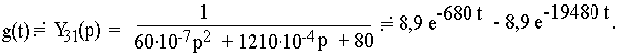
Такой же результат получим, используя найденную ранее переходную характеристику

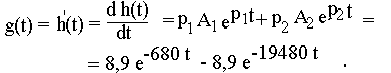
График импульсной характеристики приведен на рис.51

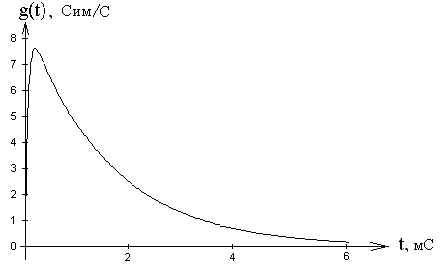
Рис. 51

Отклик цепи на первом интервале

,

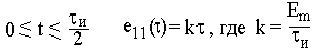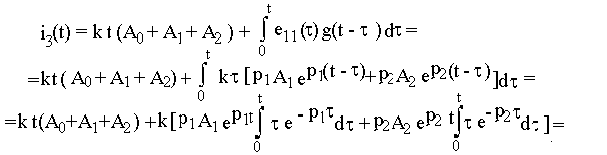
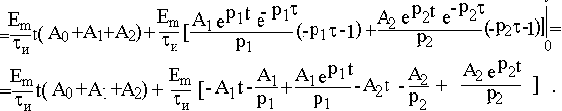
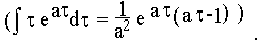
Учитывая, что А0 + А1 + А2 = h(0) = 0 и приведя подобные, получим выражение, совпадающее с приведенным в примере 6.

На интервале времени от tи /2 до tи

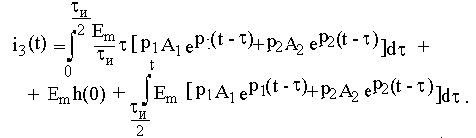
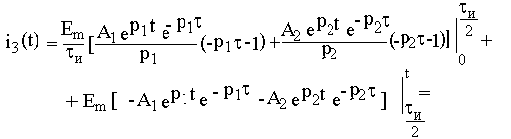
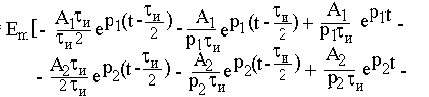
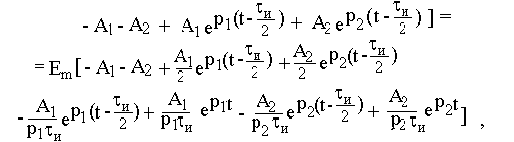
учитывая, что -А1 - А2 = А0, получим результат, совпадающий с решением в примере 6.

Расчет отклика цепи при t > tи следует проводить с учетом всего входного сигнала

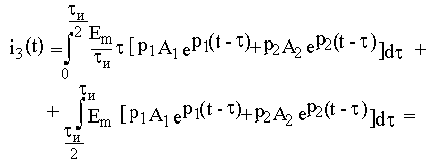
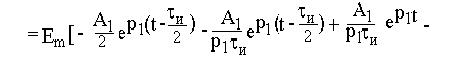
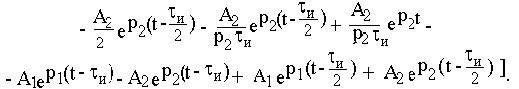
Полученные результаты полностью совпадают с откликом, рассчитанным с помощью интеграла Дюамеля.

ЛИТЕРАТУРА

1. Атабеков Г.И. Основы теории цепей.-М.: Энергия, 1969.

2. Теория линейных электрических цепей. Учеб. Пособие для радиотехнических специальностей вузов / Афанасьев Б.П., Гольдин О.Е. и др. - М.: Высш. Шк., 1973.

3. Зернов Н.В., Карпов В.Г. Теория радиотехнических цепей. - Л.: Энергия, 1972.

4. Попов В.П. Основы теории цепей. - М.: Высш. Шк., 1985.

5. Бессонов Л.А. Теоретические основы электротехники. Изд.6-е.-М.: Высш. Шк., 1973.

6. Лосев А.К. Теория линейных электрических цепей. - М.: Высш. Шк., 1987.

7. Добротворский И.Н. Теория электрических цепей. - М.: Радио и связь, 1989.