Уравнения движения в матричной форме

Уравнение движения можно получить используя принцип возможных перемещений. Подставляя в уравнение Лагранжа выражения для пот. и кинет. энергии получаем:

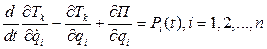
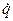– скорость; 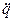- ускорение; 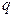- перемещение

Если подставить в это уравнение развернутые выражения для П и T_k, то получим уравнение движения в матричной форме:

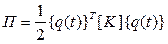
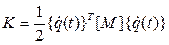
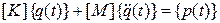
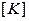- матрица жесткости; 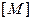- матрица масс; 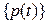- вектор обобщенных внешних воздействий

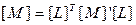(со штрихом в локальной с.к.) [L] – матрица направляющих косинусов

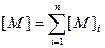, n – число к.э. в модели конструкции

С учетом сил сопротивления и опуская зависимость от t, запишем уравнение движения:

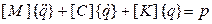
[C]-матрица демпфирования

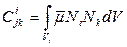, где N – ф. Эрмита; i-номер к.э.; j и k номер строки и столбца; 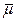- коэф. вязкого сопротивления

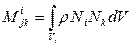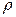; - плотность