Финальные вероятности состояний

далее будем рассматривать марков­ские процессы с дискретными состояниями и непрерывным временем.

Пример.1

Техническое устройство состоит из трёх узлов и в любой момент времени может находиться в одном из восьми состояний (рис. 1).

S₆

S₁ S₂

S₀

λ3

S₄

S₅

S₃

S₇

Рис.1

Возможные состояния устройства таковы:

S0 — все три узла исправны;

S1 — первый узел неисправен, второй и третий исправны;

S2 — второй узел неисправен, первый и третий исправны;

S3 — третий узел неисправен, первый и второй исправны;

S4— первый и третий узлы неисправны, второй исправен;

S5- второй и третий узлы неисправны, первый исправен;
S6 — первый и второй узлы неисправны, третий исправен;
S7 — все три узла неисправны.

Размеченным графом будем считать такой граф, у которого стрелками указаны переходы из одного состояния в другое, а рядом со стрелкой указана интенсивность перехода. Будем различать две интенсивности — прямую λ и обратную µ.

Тогда λ₁ λ₂ λ ₃— интенсивности потоков отказов соответственно первого, второго и третьего узлов, а µ₁ µ₂ µ.₃ — соответст­венно интенсивности потоков возвратов (ремонтов) узлов.

Если для ремонта каждого узла имеется отдельный специалист, то среднее время ремонта каждого узла есть величина постоянная и не имеет значения, один или несколько узлов вышли из строя.

На основе построенного размеченного графа (см. рис..1) создадим математическую модель.

Наше техническое устройство в соответствии с построенным графом в любой момент времени будет находиться в одном из восьми возможных состояний. Обозначим вероятность каждого i-го состояния как p_i (t), тогда

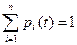(1)

Для определения вероятности каждого состояния технического устройства составим соответствующие дифференциальные уравнения. Вероятность того, что техническое устройство будет находиться в состоянии S1 (первый узел неисправен, а второй и третий узлы исправны), обозначим p₁ (t). Дадим малое приращение по времени Δt. За это малое время Δt техническое устройство либо остается в прежнем состоянии So, либо перейдет в состояние S1 из состояний S0, S4 или S6.

Определим вероятность первого случая — устройство остается в состоянии S1. В момент времени t устройство было в состоянии S1 с вероятностью p₁(t). За время Δt устройство не перейдет в любое из состояний So, S4 или S6. Суммарный поток событий, который может вывести устройство из состояния S1, будет равен λ₂ +λ₃ +µ₁ Каждый из этих потоков событий простейший, поэтому и суммарный поток также будет простейшим (все три свойства стационарности, ординарности и отсутствие последействия сохраняются).

Вероятность того, что устройство выйдет из состояния S1 будет равна p₁(t) (λ₂ +λ₃ +µ₁) Δt, а вероятность того, что останется в состоянии S1 P₁(t)(l - (λ₂ +λ₃ +µ₁) Δ t).

Теперь определим вероятность перехода устройства за время Δ t в состояние S1 из состояний S0, S4 или S6,:

Для S4 p₄(t)Δtμ₃

Для S6 p₆(t)Δtμ₂

Для S0 p₀(t)Δtλ₁

Таким образом, вероятность нахождения устройства в состоя­нии S1 будет равна:

p₁(t+Δt)=p₁(t)(1-(μ₁+λ₂+λ₃)Δt)+p₀(t)λ₁Δt+p₄(t)μ₃Δt+p₆(t)μ₂Δt

Выполним преобразования:

p₁(t+Δt)=p₁(t)- p₁(t)(μ₁+λ₂+λ₃)Δt)+p₀(t)λ₁Δt+p₄(t)μ₃Δt+p₆(t)μ₂Δt

p₁(t+Δt)- p₁(t) =- p₁(t)(μ₁+λ₂+λ₃)Δt+p₀(t)λ₁Δt+p₄(t)μ₃Δt+p₆(t)μ₂Δt

p₁(t+Δt)- p₁(t) =- p₁(t)(μ₁+λ₂+λ₃) +p₀(t)λ₁+p₄(t)μ₃+p₆(t)μ₂

Δt

Устремив Δt к нулю, получим

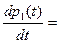-p₁(t)(μ₁+λ₂+λ₃) +p₀(t)λ₁+p₄(t)μ₃+p₆(t)μ₂ (2)

Выполнив аналогичные действия, получим 8 дифференциальных уравнений

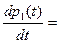
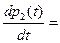
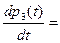
(3)

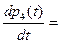
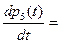
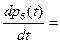
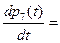
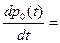
Эта система дифференциальных уравнений называется систе­мой уравнений Колмогорова. Имеем систему из восьми линейных дифференциальных уравнений с восемью неизвестными. Известно, что сумма всех вероятностей равна единице, т. е.

Ро+P1 +P2+P3+P4+P5+P6+P7 = 1. (4)

Таким образом, любое из уравнений, входящее в систему урав­нений (3), можно записать, используя уравнение (4), и найти значения вероятностей для каждого события.

Для облегчения процесса составления дифференциальных урав­нений можно применить следующее правило:

В левой части каждого уравнения следует записать производ­ную вероятности i-го состояния устройства.

В правой части сумма произведений потока событий, входя­щих в текущее состояние, умноженная на вероятность состоя­ния, из которого исходит поток, минус суммарная интенсив­ность исходящих потоков событий из текущего состояния, ум­ноженная на вероятность текущего состояния.

Когда определены вероятности событий, то встаёт вопрос: «Что будет с техническим устройством в установившемся режиме?» В ка­ком состоянии (режиме) будет находиться техническое устройство по прошествии большого периода времени, т. е. при t —> °°. Если суще­ствуют пределы вероятностей pi(t) состояний устройства и они не зависят от текущего состояния устройства, то эти пределы называют­ся финальными вероятностями состояний.

Если число состояний некоторого устройства равно n (конечное число состояний) и из каждого состояния можно перейти в другое состояние, то финальные вероятности существуют. Это положение доказывается в теории случайных процессов.

Если финальные вероятности существуют:

Lim pi(t) = Pi при i = 1, 2, 3, n, (5)

t→∞

то их сумма будет равна единице:

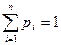(6)

Финальные вероятности показывают, какое среднее время уст­ройство будет находиться в каждом состоянии. Финальные вероят­ности находятся из системы дифференциальных уравнений, если их правые части приравнять нулю.

Зададим численные значения интенсивности потоков событий для примера 1:

λ₁= 1; λ₂ = 2; λ₃ = l; μ1 =2; μ2 = 4; μ3 = 2.

Приравняем левые части уравнений системы (3) нулю и заме­ним одно из уравнений выражением (4)

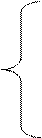
0=-p₁(μ₁+λ₂+λ₃) +p₀λ₁+p₄μ₃+p₆μ₂

0=-p₂(μ₂+λ₁+λ₃) +p₀λ₂+p₅μ₃+p₆μ₁

0=-p₃(μ₃+λ₂+λ₁) +p₀λ₃+p₄μ₁+p₅μ₂

0=-p₄(μ₁+λ₂+μ₃) +p₃λ₁+p₁λ₃+p₇μ₂

0=-p₅(λ₁+μ₂+μ₃) +p₃λ₂+p₂λ₃+p₇μ₁

0=-p₆(μ₁+μ₂+λ₃) +p₁λ₂+p₇μ₃+p₂λ₁

0=-p₀(λ₁+λ₂+λ₃) +p₁μ₁+p₃μ₃+p₂μ₂

Ро+P1 +P2+P3+P4+P5+P6+P7 = 1

Второй (отрицательный) член каждого выражения перенесем левую часть

p₁(μ₁+λ₂+λ₃)=p₀(t)λ₁+p₄(t)μ₃+p₆(t)μ₂

p₂(μ₂+λ₁+λ₃) =p₀(t)λ₂+p₅(t)μ₃+p₆(t)μ₁

p₃(μ₃+λ₂+λ₁) =p₀(t)λ₃+p₄(t)μ₁+p₅(t)μ₂

p₄(μ₁+λ₂+μ₃) =p₃(t)λ₁+p₁(t)λ₃+p₇(t)μ₂

p₅(λ₁+μ₂+μ₃) =p₃(t)λ₂+p₂(t)λ₃+p₇(t)μ₁

p₆(μ₁+μ₂+λ₃) =p₁(t)λ₂+p₇(t)μ₃+p₂(t)λ₁

p₀(λ₁+λ₂+λ₃) =p₁(t)μ₁+p₃(t)μ₃+p₂(t)μ₂

P7 = 1- Ро-P1 -P2-P3-P4-P5-P6

Подставим конкретные значения (указанные выше) прямых обратных интенсивностей

p₁(2+2+1)=1p₀+2p₄+4p₆

p₂(4+1+1) =2p₀+2p₅+2p₆

p₃(2+1+2) =1p₀+2p₄+4p₅

p₄(2+2+2) =1p₃+1p₁+4p₇

p₅(1+2+4) =2p₃+1p₂+2p₇

p₆(2+4+1) =2p₁+2p₇+1p₂

p₀(1+2+1) =2p₁+2p₃+4p₂

P7 = 1- Ро-P1 -P2-P3-P4-P5-P6

После выполнения арифметических действий получим:

5p₁=1p₀+2p₄+4p₆

6p₂ =2p₀+2p₅+2p₆

5p₃ =1p₀+2p₄+4p₅

6p₄ =1p₃+1p₁+4p₇

7p₅ =2p₃+1p₂+2p₇

7p₆ =2p₁+2p₇+1p₂

4p₀ =2p₁+2p₃+4p₂

P7 = 1- Ро-P1 -P2-P3-P4-P5-P6

Из первого уравнения выразим pl= 1/5p0+ 2/5 p4+ 4/5p6, и подставим его в остальные уравнения:

6р2 = 2р0 + 2р5 + 2р6;

5P3 = Ро+4р5 +2р4;

28/5p4=p3+4p7+1/5p0+4/5p6

7р5 = р2 + 2р3 + 2р7;

27/2p6=2/5p0+4/5p4+p2+2p7

48/5p0=4/5p4+8/5p6+4p2+2p3.

P7=1-6/5p0-p2-p3-7/5p4-p5-9/5p6

Аналогично выражаем p2=1/3P0+1/3P5 +1/3Р6 и подставляем в

оставшиеся уравнения и получаем:

5 P3 = р0+4р5 + 2р4;

28/5p4=p3+4p7+1/5p0+4/5p6

20/3p5 =1/3p0+1/3p6+2p3+2p7

79/6p6 = 11/15p0+4/5p4+1/3p5+2Р7;

124/15p0=2p3+4/5p4+4/3p5+44/15p6

p7 = 1-23/15p0-p3-7/5p4-4/3p5-32/15p6

Выражаем р3 = 1/5р0 + 4/5 р5 +2/5 р4 и подставляем в оставшиеся уравнения и получаем:

26/5p4=2/5p0+4/5p6+4p7+4/5p5

76/15p5=11/15p0+1/3p6+2p7+4/5p4

79/6p6=11/15p0+4/5p4+1/3p5+2p7

20/3p0=8/5p4+44/15p5+44/15p6

Р7 = 1-26/15p0-9/5p4-32/15p5-62/15p6

Из первого уравнения выразим р4 = 1/13 Ро + 2/13p5+2/13p6+10/13p7

и подставим в оставшиеся уравнения. После выполнения преобразований получим:

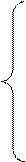
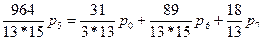
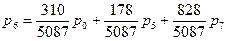
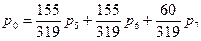
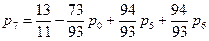
Из первого уравнения выразим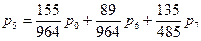

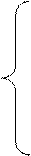И подставим в оставшиеся уравнения

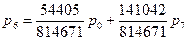
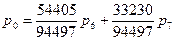
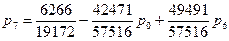
Из первого уравнения выразим Р6 и подставим в оставшиеся уравнения

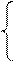
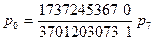
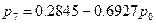
Из первого уравнения р0 и подставим в оставшиеся уравнения:

Р₇=0,2845+0,6927*0,4697р₇ р₇=0,2146

Определим остальные вероятности, подставляя полученные ре­зультаты в обратном порядке

ро = 0,4694 • 0,2146 = 0,1007;

р₆ = 0,06678*0,1007 + 0,1731 • 0,2146 = 0,04387;

р₅ = 0,1608 * 0,1007 + 0,09232 • 0,04387 + 0,2801 • 0,2146 = 0,08035;

р₄ = 0,07692 • 0,1007 + 0,1538 • 0,08035 + 0,1538 * 0,04387 + 0,7692*0,2146 = 0,08035;

р₃ = 0,2 • 0,1007 + 0,8 • 0,08035 + 0,4 • 0,1853 = 0,1585;

р₂ = 0,3333 • 0,1007 + 0,3333 • 0,08035 + 0,3333 • 0,04387 = 0,07498;

Р₁ = 0,2 • 0,1007 + 0,4 • 0,1853 + 0,8 • 0,04387 = 0,1294

. Выполним проверку. Сумма вероятностей всех событий должна быть равна единице.

Р0+Р1 + P2+ РЗ+ Р4+ Р5+ P6+ P7 = 1

0,1294 + 0,07498 + 0,1585 + 0,1853 + 0,08035 + 0,04387 + 0,1007 + + 0,2146 = 0,9877

Полученный результат меньше единицы, так как значение каж­дой вероятности было округлено.