Теология

гичная ситуация складывается к 8 в. (деятельность жутазилитов). Притом необходимая свобода для спе­куляции над «писанием» создается за счет аллегорич. истолкования последнего (талмудич. мидраши, христ. эксегеса александрийской школы, истолкование Ко­рана и хадисов у батинитов и мутазилитов). Через Т. христианства и ислама проходят типологически сходные споры о предопределении (Августин против Пелагия на Западе, Езник Кохбаци и его неизвест­ные оппоненты в Армении, «джабариты» против «ка-даритов» в исламе). Однако христ. Т., изначально раз­виваясь в греко-рим. этнич. и языковой среде, несрав­нимо раньше и полнее усваивает антич. модели филос. умозрений, что позволяет ей выработать в тринитарных и христологич. спорах 4—7 вв. (см. Патристика) такую развитую систему умозрит. догматики, к-рой не знали ни иудаизм, ни ислам (в последних Т. не отчленяется до конца от сакрального права и потому сосредоточена не на истолковании универсума, а на поведении чело­века). Эта работа церкви над догматами, в центре к-рой стоит проблема соотношения между теистически понятым абсолютом и эмпирич. миром, в основном завершается к 8 в. (787, седьмой вселенский собор). Широкая систематизация наличного «предания» на основе аристотелевских логич. схем впервые осущест­вляется христ. мыслителем, но в географич. пределах исламского региона («Изложение православной веры» Иоанна Дамаскина). Между тем антич. филос. тексты через посредство сирийских переводчиков попадают в кругозор араб, мира, и с 10 в. начинается расцвет Т. ислама (калам), достигающий высшей точки к 11 — 12 вв. (Газали и др.). В араб. Испании (Андалусии) оживляется иудейская Т., представители к-рой поль­зуются араб, языком и неоплатонич. системой поня­тий (характерен пример ибн Гебироля, сочетавшего творчество в области богослужебной поэзии на иврите с религ. философствованием на араб. яз.). В 11 в. на Западе начинается новый подъем христ. Т., отныне за­нятой не творчеством догм, а их объяснением (Ансельм Кентерберийский). В 12 в. в кругозор зап. христ. Т. (схоластики) благодаря многочисл. переводам входят тексты евр. и исламских теологов, а также Иоанна Дамаскина. Мнстич. направление Т., исходящее из данностей «внутреннего опыта» и недоверчиво отно­сящееся к логич. выкладкам, пытается дать бой схолас­тике (Бернар Клервоский против Абеляра), но выну­ждено на Западе склониться перед последней и лишь на православном Востоке со времен Симеона Нового Бого­слова оказывается господином положения (концепция Т. как «умного делания»). Внутри интеллектуального мира схоластики создается международная и даже ■(в известных пределах) межвероисповедная иудео-христианско-исламская общность: в те самые века, когда в Испании распря христианства и ислама реша­лась мечом, мусульманин аль-Газали («Альгацель») и иудей ибн Гебироль («Авицеброн») служили для ка-толич. Т. школьными авторитетами (в свою очередь тексты последней часто переводились на иврит и ис­пользовались в полемике раввинских школ). Эта эпоха Т. получила в 13 в. свое завершение в католич. системе Фомы Аквинского. В последующие века Т. ислама и иудаизма не создает ничего нового, в то время как христ. Т. работает над последоват. деструкцией схо-ластич. здания (Иоанн Дуне Скот, Оккам): синтез Но­вого завета и Аристотеля, достигнутый предыдущими поколениями, не удовлетворял ни тех, кто стоял на стороне мирских тенденций гуманизма, ни тех, кто пы­тался в новых условиях возродить серьезное отношение к принципу веры. Аверроистская теория двойственной истины, пришедшая из философии ислама и отвергну­тая Фомой Аквинским во имя безусловной гармонии между логикой и верой, приобретала все больше явных и скрытых сторонников. Лютер решительно отверг

саму идею Т. как умозрит. дисциплины, исследующей «бога в аспекте божественности»; для Лютера предме­том Т. является исключительно личностные взаимоот­ношения нуждающегося в боге человека и окликающе­го человека бога; последний неуловим для абстрактных построений н раскрыт лишь в конкретном, внелогич. «событии» крестной смерти Христа (т. н. Т. креста). Т., к-рая для Фомы Аквинского была «наукой скорее спекулятивной, нежели практической» (S. Theol. I, a. 4), для Лютера есть всецело практич. дисциплина, обя­занная заниматься не богом-в-себе, но богом-для-нас (ср. J. Hessen, Platonismus und Prophetismus..., Munch., 1939, S. 182). Т. зр. Лютера Меланхтон выра­жает в таких словах: «Познавать Христа означает поз­навать его благодеяния, а не исследовать его естества и модусы воплощения» (введение к 1 изд. «Loci commu­nes», 1521). Однако в дальнейшем тот же Меланхтон воз­вращается к арпстотелианско-схоластич. наследию, формальные мыслит, схемы к-рого приемлются в рав­ной степени догматич. Т. контрреформации (Суарес, Беллармин) и протестантизма (Герардт), пока в своем самоисчерпанин не становятся к 18 в. расхожей монетой католических, протестантских и православных школьных догматик. Просвещение вытесняет дегради­рованную Т. за границы филос. жизни. Шлейермахер пы­тается приспособить Т. к нуждам бурж. культуры, ус­воив для нее стиль просветительского мировосприятия. Напротив, Къеркегор, осмыслив кризис самой бурж. культуры, ищет выхода в запоздалой реализации заве­та Лютера: библейская вера, порвавшая противоес-теств. союз с греч. рационализмом и осознавшая себя как чистое возвещение, без резонов и доводов апелли­рующее к личностному выбору. Линия Кьеркегора бы­ла продолжена в 20 в. теологией диалектической; к ней примыкает движение за демифологизацию веры, родившееся из теорий Бультмана и исходящее из осознания противоречия между совр. сциентистским мышлением и знаковой системой новозаветного мифа. Это движение, до последнего времени развивавшееся в рамках протестантской Т. (ср. нашумевшую книгу епископа Робинсона «Честно перед богом»), перешло и в католич. Т. и притом в связи с попытками обществ, переориентации католицизма; ср. характерное заяв­ление иезуитского теолога Г. Руиса: «Чтобы быть чест­ными..., мы обязаны признать, что мифы... удобны и служат консервации тех великих политико-социаль­ных строений, внутри которых средиземноморский мир компрометировал себя во время римской импе­рии, во времена средневекового христианства и во времена грандиозных колониальных предприятий сов­ременной эпохи» (цит. по книге: Garaudy R., Metz J.B., R ahnerK.,DerDialog...,Reinbeck, 1966, S. 44—45).

Лит.: Маркс К. иЭнгельс Ф.,0 религии, М.,
1955; Архимандрит Сильвестр, Опыт право­
славного догматич. богословия, т. 1 — 5, К., 1884 — 91;
Трубецкой С. Н., Учение о логосе в его истории,
[2 изд.], Собр. соч., т. 4, М., 1906; Флоренский П. А.,
Столп и утверждение истины, м., 1914; Булгаков С. Н.,
Свет невечерний. Созерцания и умозрения, М., 1917; К р ы в е-
лев И. А., Совр. богословие и наука, М., 1959; Лева­
да Ю. А., Социальная природа религии, М., 1965; Во­
просы науч. атеизма, вып. 2, 6, М., 1966—68; Г а б и н-
с к и й Г. А., Критика христ. апологетики, М., 1967;
Аверинцев С, Жак Маритен, неотомизм, католич.
Т. иск-ва, «Вопр. лит-ры», 1968, №10, с. 126—43; Н а г-
п а с k A von, Die Entstehung der christlichen Theologie
und des kirchlichen Dogmas, Gotlia, 1927; G 1 a w e W., Die
Hellenisierung des Christentums in der Geschiehte der Theolo­
gie von Luther bis auf die Gegenwart, В., 1912; К о e p g e n G.,
Die Gnosis des Christentums, Salzburg, 1940; Hessen J.,
Griechische Oder biblische Theologie? Das Problem der Hel-
leniesierung des Christentums in neuer Beleuchtung, Lpz.,
1956; Wagner H., Der Mytbos und das Wort. Ein Beitrag
zur Frage der Verkundigung fur den gegenwfirtigen Menschen,
Lpz., 1957; Laeuchli S., The language of Faith. An intro­
duction to the semantic dilemma of the early church, N.Y.,
1962; The later Heidegger and theology, ed. by J. M. Robinson
and J. B. Cobb, N.Y., 1963. С. Аверинцев. Москва.

ТЕОЛОГИЯ ДИАЛЕКТИЧЕСКАЯ — ТЕОРЕМА 203

ТЕОЛОГИЯ ДИАЛЕКТИЧЕСКАЯ, теология криз и с а,— ведущее направление в европ. теологии протестантизма 20-х— 30-х гг. 20 в., развивавшееся в контакте с ранним немецким экзистенциализмом и близкое к нему по генезису и установкам (напр., в стремлении опереться на наследие Къеркегора и др.). Толчком к возникновению Т. д. был глубокий кризис устоев европ. бурж. цивилизации, выявившийся в свя­зи с 1-й мировой войной и ее последствиями. Прин­ципы нового течения были сформулированы в 1921 — 1922 в работах К. Барта, Э. Бруннера, Р. Бультмана, Ф. Гогартена, Э. Турнейзена, а к осени 1923 был соз­дан его печатный орган «Zwischen den Zeiten» («Между временами»). Манифестом Т. д. явилось 1-е изд. кн. К. Барта «Толкование на послание апостола Павла к римлянам» («Der Romerbrief», Munch., 1922). Путь Т.д. задуман ее инициаторами как «диалектический»: путь к утверждению через отрицание и противоречие. Ис­ходный пункт Т. д.— безнадежность всех попыток определить содержание веры через к.-л. теологич. или культовые манипуляции, вообще через «религию», к-рую Т. д. резко противопоставляет «вере». «Религия» порочна потому, что стремится «связать» несвязуемое: «не-наглядного» и «не-вещного» бога с наглядным п вещным миром человеч. интеллекта и воображения (ср. P. Tillich, Die Uberwindung des Religionsbegriffes, «Kantstudien», 1922, Bd 27, S. 446—69). Застывание еванг. веры в «христ. религию» рассматривается как возврат к тому, что было исторически преодолено. Усматривая в религии иллюзию, благодаря к-рой человек под видом бога получает собств. мистифици­рованный образ, Т. д. готова солидаризироваться с атеистич. антропологизмом Фейербаха. Однако «нет» Т. д.— это не «нет» атеизма, а «нет» отрицательной тео­логии: отрицая религию как сумму предметных пред­ставлений и действий, Т. д. утверждает веру в абсо­лютно трансцендентного по отношению ко всему чело­веческому бога. Перед таким богом человек в любом своем совершенстве (и даже в вере) обречен стоять с пустыми руками; бог есть «критическое отрицание» всего, «совершенно не-предметный источник кри­зиса всякой предметности, судия, не-бытие мира» (BarthR., Der Romerbrief, 1922, S. 57). Краски для описания трансцендентности бога Т. д. заимствует у разработанного Р. Отто и неокантианской религ. философией понятия «совершенно иного», переосмыс­ляя его в духе доктрины Кальвина о запредельном «ве­личии божьем» и учения Лютера о боге как огненном море гнева, истребляющем все человеческое. Именно в гневе бога Т. д. видит единств, возможность ми­лости бога, в его немыслимости — единств, возмож­ность его мыслить. Человек может обрести отношение к богу лишь на пределе своего бытия, лишь будучи «снят» богом в диалектич. отрицании, происходящем че­рез «свершение» Голгофы. В той мере, в какой человек тождествен себе, он не может веровать, а в той мере, в какой он верует, он не тождествен себе («Лишь через веру я есмь то, что я не (!) есмь» — В а г t h К., там же, S. 126).

При таких предпосылках положение теологии ста­новится весьма драматическим: она ощущает себя между только что отвергнутой предметностью и пустой беспредметностью, между фальшивым утверждением и бессодержат. отрицанием. Выход из этой ситуации усматривается в обращении к откровенно многосмыс-ленным формулировкам: «остается одно — поставить утверждение и отрицание во взаимную связь, прояс­нять „да" через „нет" и „нет" через „да"» (Gogarten F., Das Wort Gottes und Schriften, В., 1936, S. 137). Бли­зость этой установки к методу философствования Хайдеггера и Ясперса очевидна.

В псторич. перспективе учение Т. д. предстает как возвращение к осн. идейным мотивам инициаторов Ре-

формации — Лютера и Кальвина. Отвержение «рели­гии» — это логич. предел лютеровского отвержения «оправдания делами». Чтобы ответить на вопрос, на к-рый впервые отвечал Лютер: как вера может жить рядом с новоевроп. бурж. нигилизмом, Т. д. дол­жна была покончить с либеральным протестантизмом 19 в., растворявшим религию в стихии безрелиг. ци­вилизации, откровение — в истории, веру — в психо­логии. Возвращаясь к истокам протестантизма, Т. д. оказалась в русле довольно широкого течения протес­тантской т. н. неоортодоксии.

Распад течения Т. д. был связан, во-первых, с по-литич. событиями 30-х гг.: если Барт и Тиллих стали провозвестниками христ. сопротивления гитлеризму, то Гогартен примкнул к пронацистскому течению т.н. «немецких христиан». Во-вторых, неустойчивое равно­весие «да» и «нет» в доктрине Т.д. легко нарушалось в том или ином направлении. Бультман пошел от Т. д. к провозглашению «демифологизации» христ. учения, Тиллих наметил возможности отказа от импе­ративы веры в бога, широко используемые новейшей протестантской теологией, и попытался включить в теологию мировоззренч. элементы чисто секулярного происхождения, а Бруннер перешел к построению но­вой «естественной теологии», что вызвало резкую от­поведь Барта. В США эпилогом к европ. истории Т. д. явилась деятельность Р. Нибура, заимствующего у своих нем. предшественников критику теологич. либерализма и социального оптимизма и т. п.

С. Аверинцев. Москва

ТЕОРЕМА (греч. десорпиа, от дешргсо — рассмат­риваю, исследую) — доказанное предложение нек-рой дедуктивной теории. В содержательных (неформаль­ных) теориях Т. доказываются весьма приблизительно фиксируемыми (чаще — молчаливо подразумеваемыми) средствами «обычной логики» и часто противопоставля­ются «не требующим доказательства» (принимаемым за истинные в силу своей «очевидности») аксиомам. Впрочем, если даже точный перечень аксиом и не фик­сируется, то в (полном) доказательстве каждой Т. все же проводится различение посылок на доказанные ранее Т. и аксиомы; фактически статус последних мо­жет специально и не оговариваться — этой цели может служить к.-л. косвенная мотивировка применяемой аргументации или даже сам факт умолчания о при­чинах, позволяющих пользоваться данной посылкой. Такой, напр., характер имеют Т. в большей части учеб­ных руководств по различным разделам (неаксиомати-зированной) математики. Если же данная дисциплина строится на аксиоматич. основе (хотя бы и в содержат, форме), то (нелогические) аксиомы явно перечисляют­ся, как, напр., при изложении различных разделов абстрактной алгебры или топологии, а из нематематич. дисциплин — теоретич. механики или термодинамики.

В формальных аксиоматич. системах (исчислениях) Т. наз. доказуемая формула, т. е. формула, выводи­мая по правилам вывода данной системы из ее аксиом. При этом аксиомы теории также причисляются к Т. (доказательство каждой такой Т. состоит из одной фор­мулы — из нее самой); это вполне естеств. соглашение оправдывается не только индуктивным характером определения понятия доказательства (см. раздел Ре­курсивные п индуктивные определения в ст. Опре­деление), но и тем обстоятельством, что один и тот же класс доказуемых формул может задаваться раз­личными системами аксиом, и в ряде случаев выбор определенных формул (фиксированной теории) в каче­стве аксиом диктуется чисто технич. соображениями, так что противопоставление к.-л. аксиомы и (дедук­тивно) эквивалентной ей Т. оказывается весьма отно­сительным.

Иногда Т., играющие вспомогат. роль и нужные лишь для доказательства к.-л. другой Т., наз. лемма-

204 ТЕОРЕМА О ДЕДУКЦИИ—ТЕОРЕТИКО-МНОЖЕСТВЕННАЯ ЛОГИКА

ми; Т., доказательство к-рых весьма просто получается посредством ссылки на другие Т., наз. с л е д с т в и-я м и этих других Т. Ввиду недостаточной опреде­ленности таких понятий, как «вспомогательный» и «просто», термины «лемма» и «следствие» также носят несколько условный характер, и эти наименования свидетельствуют не столько о характере самих Т., сколько о стиле или уровне изложения предмета.

Т., доказываемые содержат, средствами метатео­
рии к.-л. теории, наз. м е т а т е о р е м а м и, отно­
сящимися к данной («предметной») теории. Примеры
метатеорем: теорема о дедукции для исчисления
высказываний или предикатов, теорема Гёделя о
полноте исчисления предикатов, теорема Гёделя
о неполноте формальных систем, включающих фор­
мальную арифметику, теорема Чёрча о неразрешимо­
сти разрешения проблемы для исчисления предикатов,
теорема Тарского о невыразимости (неопределимо­
сти, см. Определимость) предиката истинности для
широкого класса логич. исчислений средствами самого
исчисления (см. Логическая истинность) и др. Вообще
метатеоремами являются любые Т. о Т., какими бы
средствами и в рамках какой бы теории они не дока­
зывались; примерами могут служить т. н. принципы
двойственности, играющие важную роль во мн. разде­
лах математики. См. Вывод (в математической логике),
Доказательство, Метод аксиоматический и лит. при
ЭТИХ статьях. Ю. Гастев. Москва.

ТЕОРЕМА О ДЕДУКЦИИ, теорема дедук-ц и и,— одно из важнейших содержательных утвер­ждений математической логики, определяющее связь между логически правильными (аподиктическими) рас­суждениями (или умозаключениями, или выводами) и законами (доказуемыми формулами) логики, лежащими в их основе. Прообраз Т. од. был известен еще стои­кам (см. J.B. Mates, Stoic logic, Berk.— Los Ang., 1953) в виде общего принципа связи между выводи­мостью и импликацией. Как (металогическая) тео­рема логических исчислений Т. о д. была сформулиро­вана независимо франц. математиком Ж. Эрбраном (1928) и А. Тарским (1930) и доказана Эрбраном (1930) для исчислений, включающих положительное нмплн-кативнсе исчисление высказываний Гильберта [см. Положительная логика, аксиомы 2.1) и 2.2)]. Форму­лировки Т. о д. зависят, вообще говоря, от того как в том или ином исчислении определяются понятия «вы­водимость» и «импликация»; поэтому всегда следует иметь в виду тот или иной вариант Т. о д.

Интуитивно ясным примером Т. о д. для исчисления высказываний может служить следующая ее форму­лировка: (1) если из аксиом исчисления и к.-л. допу­щения (гипотезы) А, добавленного к числу аксиом, по правилам исчисления выводимо В, то в этом исчислении доказуемо (выводимо только из аксиом) условие (имп­ликация) AzjB, означающее, что если доказано А, то доказано и В. Др. словами, данная формулировка Т. о д. означает, что при наличии отношения логич. следования между любой (произвольной) посылкой А и заключением В, доказуемость В р е л я т и в и з и-р у е т с я условием доказуемости А, или, что то же, доказательство В сводится (см. Сводимость) к доказательству А. Идея такого сведения, являющегося отражением аналитического процесса реше­ния матем. и логич. задач, очевидна: после того как установлено, что В является следствием А — на что указывает факт выводимости В из А, — совершенно ясно, что В конечно же будет доказано, если удастся показать, что А — теорема исчисления. Это вытекает из обратного утверждения, отражающего уже синте­тическую часть решения: по правилу modus po-nens, если А доказуемая формула, то из А и доказан­ного в силу Т. о д. утверждения AzsB следует, что В доказано. Поэтому Т. о д. часто называют обращением

modus ponens и, основываясь на указанной взаимной связи между выводимостью и импликацией, формули­руют так: (2) необходимым и достаточным условием для категорического утверждения А_х, А_г,..., А_п\ — В (т. е. для утверждения о выводимости в нек-ром ис­числении по его правилам заключения В из посылок A_lt A₂,..., А_п) является логическая истинность (до­казуемость в этом исчислении) условного утверждения A_xzd(A p(...a(jl_nDfi)...)). Эта формулировка Т. о д. фиксирует ту, замеченную еще стоиками, особую роль, к-рую в логике высказываний играют ее законы при определении (проверке) логич. правильности наших рассуждений: относительно любого утверждения о выводимости заключения В из посылок А_х, Л₂,..., А_п вопрос о его истинности решается разысканием среди законов логики закона A_xzi(A^(...z^(A_nZiB)...)).

Различение понятий «выводимость» и «доказуемость» (соответственно «вывод» и «доказательство») в приве­денных выше формулировках Т. о д. восходит к традиц. различению между понятиями «формальная правиль­ность» и «истинность». Пусть В выведено из к.-л. до­пущений (гипотез) А_г,...,А_т. Доказано ли В? В общем случае очевидно нет, потому что допущения могут быть любыми, в том числе и ложными, а понятие логич. вы­вода определяется, как правило, так, что из лжи можно вывести любое, в том числе и ложное, заклю­чение. Для того чтобы В было доказано, необходимо, чтобы В следовало из заведомо истинных (или при­нимаемых за истинные) посылок.

Т. о д. имеет место только для исчислений логисти­ческого типа, в к-рых вывод опирается на «абсолют­ные» допущения (см. Посылка) — аксиомы (или схемы аксиом). Это объясняется, конечно, не наличием слова «доказуема» в приведенных формулировках теоремы [этого может и не быть: напр., С. К. Клини (1952) и А. Чёрч (1956) используют др. терминологию, так что в их формулировках Т. о д. выражает связь между выводимостью одной формулы и выводимостью (же) нек-рой др. формулы], а просто тем, что Т. о д.— это теорема, т. е. утверждение, доказываемое на основе аксиом. В исчислениях без аксиом (в натуральных ис­числениях) вместо Т. о д. вводится в качестве основного (или обосновывается в качестве производного) правило введения импликации — в нек-ром смысле аналог Т. о д.: если общий принцип (идею), выражае­мый Т. о д., рассматривать независимо от того, что это принцип (идея) теоремы, то его можно постулиро­вать в форме правила (Г. Генцен, С. Ящьковский, 1934), к-рое равносильно названным выше аксиомам 2.1) и 2.2) положительной логики.

Лит.: Т а р с к и й А., Введение в логику и методологию
дедуктивных наук, М.. 1948, е. 173—79; Клини С. К.,
Введение в метаматематику, пер. с англ.. М._? 1957, с. 84—91;
Чёрч А., Введение в математическую логику, пер. с англ.,
т. 1, М., 1960, с. 80, 186, 287; Г у д с т е и н Р. Л., Математи­
ческая логика, пер. с англ., М., 1961, с. 35—37, 43—44;
Н о в и к о в П. С, Элементы математической логики, М., 1959,
с. 82—85,221—25; Столл Р. Р., Множества. Логика. Аксио­
матические теории, пер. с англ., М., 1968, с. 171—72; Л и н-
д о н Р., Заметки по логике, пер. с англ., М., 1968, с. 72—73;
Herbrand J., Recherches sur la theorie de la demonstra­
tion, Warsz., 1930; Pogorzelski W. A., Przeglsid twi-
erdzert о dedukcji dla rachunkdw zdari, «Studia Logica», 1964,
t. 15. M. Новосёлов. Москва.

ТЕОРЕТИКО-МНОЖЕСТВЕННАЯ ЛОГИКА (т е о-

р е т и к о-м ножественная логика пре­дикатов) — логика, трактуемая с т. зр. теории множеств. К Т.-м. л. в широком смысле можно отнести любые интерпретации логич. исчислений, в основу к-рых положено объемное, экстенсиональное понимание суждений, когда суждения отождествляют­ся (или ставятся во взаимно-однозначное соответствие) с классами (множествами) объектов, для к-рых они истинны; при этом каждому логич. соотношению будет очевидным образом сопоставляться нек-рое определен­ное (и притом единственное) соотношение между клас-

ТЕОРЕТИКО-МНОЖЕСТВЕННАЯ ЛОГИКА— ТЕОРИЯ

сами (множествами). При такой теоретико-множеств. интерпретации логика высказываний по существу сов­падает с логикой классов (алгеброй множеств — см. Алгебра логики). Изоморфизм между логикой клас­сов (алгеброй множеств) и логикой высказываний ле­жит в основе аналогий обеих этих систем с разно­образными абстрактными и реальными системами (ней­ронные сети, релейно-контактные схемы, «двоичная арифметика» электронно-вычислительных машин и др.), обусловивших плодотворность взаимного прило­жения методов и результатов каждой из этих теорий к любой из остальных (см. Кибернетика).

Т.-м. л. в узком смысле представляет собой использование «наивных» (идущих от Г. Кантора) тео­ретико-множеств. концепций (в т. ч. абстракции ак­туальной бесконечности) в качестве средств метатео-ретического исследования (см. Метатеория) логич. и логико-матем. исчислений, преимущественно (прикладного) предикатов исчисления. Именно допу­щение таких «нефинитных» (см. Финитизм) средств отличает Т.-м. л. в данном понимании от метама­тематики Д. Гильберта; применение их для решения такой важнейшей проблемы оснований математики и логики, как непротиворечивость, не только не согла­суется с «финитной установкой» Гильберта, но и по существу приводит (хотя бы ввиду наличия в теории множеств парадоксов) к порочному кругу. Это обстоя­тельство, однако, не снимает задачи теоретико-мно­жеств. истолкования теорем (прикладного) исчисления предикатов — хотя бы потому, что для значит, боль­шинства математиков теория множеств остается обще­признанным и «универсальным» источником пост­роения моделей формализованной математики и «ло­гической» (во всяком случае — концептуальной) ба­зой большей части математики содержательной. К тому же, кроме непротиворечивости, при изучении исчисления предикатов и базирующихся на нем тео­рий встает ряд проблем, имеющих объективный (хотя и несколько «платонистский») смысл и интерес, но не допускающих постановки (не говоря уже о решении) в финитных (и вообще конструктивных — см. Кон­структивное направление) терминах. К числу таких проблем относится прежде всего проблема полноты дедуктивной исчисления предикатов, понимаемой в содержательно-семантическом смысле, и связанное с этой проблемой понятие «произвольной интерпрета­ции», носящее нефинитный, неконструктивный харак­тер. Тем более это относится к представлению о «сово­купности всех интерпретаций» и определяемому с по­мощью этого представления понятию общезна­чимости суждения. Т. о., к Т.-м. л. (а не к мета­математике!) относятся, напр., и теорема Гёделя о пол­ноте исчисления предикатов, и теорема Лёвенхейма — Сколема об интерпретируемости на натуральном ряде чисел любой непротиворечивой теории. Еще более выраженный теоретико-множеств. характер носят ре­зультаты, относящиеся к понятию «категоричности относительно данной мощности», т. е. изоморфизма всех моделей данной мощности (см. Категоричность системы аксиом).

Термин «Т.-м.л.» часто применяется еще в «собст­венном» смысле: так именуют совокупность теоретико-множеств. методов и результатов, относящихся к (узко­му) исчислению предикатов (как метатеоретических — типа, напр., уже упомянутой теоремы Гёделя, так и относящихся к интерпретациям; исчисление одно­местных предикатов интерпретируется в этом смысле как логика классов, а исчисление многоместных пре­дикатов — как теория множеств упорядоченных конеч­ных наборов индивидов). Эту богатую результатами и интенсивно развивающуюся (прежде всего силами школ А. Тарского, А. И. Мальцева и А. Робинсона) ветвь матем. логики, использующую гл. обр. алгеб-

раич. методы, в настоящее время называют обычно теорией моделей.

Лит.: К лини С. К., Введение в метаматематику, пер.
с англ., М., 1957, §37, 72,73, 75, 76; Робинсон А.,
Введение в теорию моделей и метаматематику алгебры, пер.
с англ., М., 1967; Ершов Ю. Л. [и др.], Элементарные
теории, «Успехи математич. наук», 1965, т. 20, вып. 4 (124),
с. 37—108. Ю. Гастев. Москва.

ТЕОРИЯ (греч. ftecopi'a, от frecopico — рассматри­ваю, исследую)—1) В широком смысле — форма дея­тельности общественно развитого человека, направлен­ная на получение знания о природной и социальной действительности и вместе с практикой образующая совокупную деятельность общества. В этом смысле понятие Т. является синонимом обществ, сознания в наиболее высоких и развитых формах его организации; как высший продукт организованного мышления она опосредует всякое отношение человека к действитель­ности и является условием подлинно сознат. преобра­зования последней. 2) В узком смысле — форма до­стоверного науч. знания о нек-рой совокупности объек­тов, представляющая собой систему взаимосвязанных утверждений и доказательств и содержащая методы объяснения и предсказания явлений данной предмет­ной области. В этом смысле Т. противопоставляется эмпирич. знанию и отличается от него, во-первых, дос­товерностью содержащегося в ней науч. знания, обес­печиваемой получением этого знания в соответствии с существующими науч. стандартами и выражающейся в его внутр. непротиворечивости, реализации его про­верки на истинность и т. д.; во-вторых, тем, что Т. дает обобщенное описание исследуемых в ней явлений, фор­мулирование в ее рамках общих законов, к-рые не только описывают определ. круг явлений, но и дают их объяснение и содержат возможность предсказания но­вых,еще не изученных фактов; в-третьих, выделением в составе Т. множества исходных утверждений и мно­жества утверждений, получаемых из исходных путем вывода, доказательства, причем сам процесс доказа­тельства подчиняется особым логич. закономерностям, к-рые формулируются для данной Т. или для определ. класса Т. Благодаря этим особенностям Т. отлича­ется от др. форм знания тем, что в ней возможен пе­реход от одного утверждения к другому без непо-средств. обращения к чувств, опыту; в этом, в частно­сти, коренится источник предсказат. силы Т.

В истории философии термин «Т.» долгое время употреблялся только в широком смысле, в контексте анализа общей структуры человеч. деятельности (исто­рию этого аспекта Т. см. в ст. Практика), хотя методо-логпч. проблематика построения теоретич. систем бы­ла поставлена уже в «Началах» Эвклида. Обсуждение проблем Т. в узком смысле начинается с 18 в. (А. Фер-гюсон, Кант) и приобретает интенсивный характер с конца 19 в. в связи с появлением совр. средств логич. анализа. При этом проблема познават. ценности Т. рассматривается в русле различных концепций тео­рии познания (Мах, Джемс, Пирсон, Оствальд, Пуан­каре, Дюгем, Гуссерль и др.), а второй большой круг вопросов связан с анализом логич. структуры Т. (эта проблематика особенно широко разрабатывается в рамках неопозитивизма.). В наст, время различные аспекты сущности и функций Т. изучаются филосо­фией, логикой, историей и психологией науки и др. дисциплинами.

В строении Т., взятой в общем, абстрактно-логич. ви­де, можно выделить следующие осн. компоненты: 1) исходную эмпирич. основу Т., в к-рую входит множество зафиксированных в науке (в данной ее отрасли) фак­тов, проведенных экспериментов и пр., к-рые хотя и получили уже нек-рое описание, но еще ждут своего объяснения, теоретич. интерпретации; 2) исходную тео­ретич. основу Т.— множество допущений, постулатов, аксиом, общих законов Т.; 3) логику Т.— множество

ТЕОРИЯ

допустимых в рамках Т. правил логич.. вывода и до­казательства; 4) совокупность выведенных в Т. след­ствий, теорем, утверждений с их доказательствами — наибольшая по объему часть Т., к-рая п выполняет основные функции теоретического знания, составляя «тело» Т.

Общая структура Т. по-разному выражается в раз­ных типах Т. Один из наиболее широких классов совр. научных Т. составляют описательные Т. (их иногда называют эмпирическими). Таковы эволюц. Т. в биологии Дарвина, фпзиологич. Т., созданная И. П. Павловым, различные совр. исихологич. Т., традицион­ные лингвистич. Т. и т. д. Такая Т. непосредственно описывает определ. группу объектов; ее эмпирич. базис обычно весьма обширен, а сама Т. решает прежде всего задачу упорядочивания относящихся к ней фактов. Общие законы, формулируемые в Т. этого типа, пред­ставляют собой генерализацию эмпирич. материала и вводятся в Т. не в ее начальных пунктах, а в зависи­мости от потребностей развертывания Т. Эти Т. фор­мулируются в обычных естеств. языках с привлече­нием лишь спец. терминологии соответствующей об­ласти знания. В них обычно не формулируются явным образом правила используемой логики и не проверяет­ся корректность проводимых доказательств. Описат. Т. носят по преимуществу качественный характер, что определяет их ограниченность, связанную с невозмож­ностью количественно охарактеризовать то или иное явление.

Второй тип Т.— математизированные науч. Т., ис­пользующие аппарат и модели математики. В матем. модели конструируется особый идеальный объект, за­мещающий и представляющий нек-рый реальный объект. Математизированные Т. наиболее специфичны для совр. теоретич. знания. Их ценность повышается в связи с тем, что нередко используемые в них матем. модели допускают не одну, а несколько интерпрета­ций, в т. ч. и на объекты разной природы, лишь бы они удовлетворяли построенной Т. (напр., модели управ­ления запасами, созданные в исследовании операций, с равным успехом применяются к процессу получения и использования оборотного капитала, найму и обу­чению рабочей силы, к анализу перспектив расшире­ния производств, мощностей и т. д.). Но и математи­зированные Т. не связаны с эксплицитным заданием их логики. Широкое использование в этих Т. ма-тематич. средств выдвигает сложную проблему их интерпретации (ее решение в самих Т., как правило, не содержится) и ведет к тому, что вопрос об их обос­новании может быть решен при условии решения вопроса об обоснованности используемых в них раз­делов математики.

Задача обоснования математики и др. формальных наук привела к построению Т. третьего типа — их можно назвать дедуктивными теоретич. системами. Первой такой системой явились «Начала» Эвклида, построенные с помощью аксиоматич. метода. Исход­ная теоретич. основа таких Т. формулируется в их на­чале и затем в Т. включаются лишь те утверждения, к-рые могут быть получены логически из этой основы. Все логич. средства, используемые в этих Т., строго фиксируются, и доказательства Т. строятся в соот­ветствии с этими средствами. Дедуктивные Т. строятся обычно в особых формальных языках. Обладая большой общностью, такие Т. вместе с тем остро ставят пробле­му их интерпретации, к-рая является условием превра­щения формального языка в знание в собств. смысле слова. В совр. науке наиболее употребительны след. еиды дедуктивных Т.:1) аксиоматические, когда ряд предложений Т. принимается без доказательства (ак­сиомы), входящие в них понятия являются неопреде­ляемыми в данной Т., а все остальное знание выводится из аксиом по заранее формулируемым логич. прави-

лам. Последующее успешное применение аксиоматич. Т. в конечном счете обосновывает истинность ее аксиом. 2) Конструктивные, когда сводят до минимума прини­маемые без доказательства утверждения и все объекты и утверждения Т. вводят лишь на основе конструи­рования, реально осуществляемого или возможного на основе имеющихся средств. 3) Гипотетико-дедуктив-ные, к-рые удовлетворяют всем принципам аксиома­тич. построения, но, кроме того, нек-рому множеству утверждений Т. дается непосредств. эмпирич. интер­претация, а остальные утверждения получают кос­венную интерпретацию благодаря своей логич. связи с первыми (этот вид Т. широко применяется при по­строении Т. в областях знания, основанных на опыте н эксперименте).

Строго построенные дедуктивные Т. удовлетворяют всем требованиям, предъявляемым теоретич. знанию совр. логикой и методологией науки. Однако существу­ют принципиальные трудности создания таких Т., оп­ределяемые границами возможной формализации пред­мета Т. Поэтому для теоретич. воспроизведения слож­ных развивающихся объектов действительности ис­пользуются др. методы, в частности метод восхожде­ния от абстрактного к конкретному — форма пост­роения Т., разработанная и примененная Марксом в «Капитале» и объединяющая в себе описательные, модельные, строго дедуктивные и др. компоненты.

Кроме приведенной, в совр. логике рассматриваются и др. схемы классификации Т. Одна из них основана на различении Т. по степени их «закрытости». «Закрытые» Т. формулируются т. о., что имеется ограниченное число исходных утверждений и все остальные утверж­дения Т. могут быть получены из исходных с помощью нек-рых правил вывода (аксиоматич. Т.). Для дос­таточно богатых Т. нельзя построить полностью фор­мализованной аксиоматич. системы, т. к. в них всегда имеются содержательно-истинные, но алгорит­мически не разрешимые (в рамках данной Т.) выска­зывания. В «открытых» Т. не налагаются никакие ог­раничения на число исходных высказываний; по дос­тижении нек-рой степени развития они могут быть пе­реформулированы в «закрытые» Т. Распространенная классификация Т. по предметным областям представ­ляет часть более общей проблемы классификации наук. Иногда Т. делят на объясняющие и описывающие (фе­номенологические): первые характеризуют ь понятиях закономерности нек-рой области мира, а вторые только дают формальный аппарат, позволяющий делать пред­сказания о вероятности наступления нек-рых фикси­руемых в чувств, опыте событий. Как и все другие, эта классификация условна.

Во всех классификациях Т. так или иначе выступает тот факт, что п с формальной, и с содержат, стороны Т. существенно опирается на внетеоретич. средства. Этот факт наиболее исследован с т. зр. отношения теоретич. и эмпирич. знания или, иначе, соотношения «языка Т.» и «языка наблюдения», системы теоретич. объектов и системы эмпирич. объектов. Осн. проблема состоит здесь в том, что построение теоретич. объекта предпо­лагает не только отвлечение от нек-рых сторон дейст­вительности, но и приписывание объекту таких свойств, к-рые заведомо отсутствуют у реальных предметов (напр., отсутствие протяженности у точки в математи­ке). Опираясь на эту нетождественность теоретич. объ­ектов с предметами внешнего мира, являющуюся одной из коренных особенностей Т., неопозитивисты пыта­лись найти способы сведения выражений Т. к выраже­ниям, сформулированным на «языке наблюдения», — ре­шить проблему эмпирич. интерпретации Т. Однако эти попытки приводили к выводу, что «сопоставима с опы­том» путем интерпретации лишь небольшая часть теоре­тич. объектов, тогда как др. объектам (напр., электро­нам) в чувств, опыте нечего сопоставить. Это обстоя-

ТЕОРИЯ—ТЕОРИЯ ГРАФОВ

тельство истолковывалось как свидетельство произ­вольности теоретич. конструкций, а Т. квалифициро­валась как «чистый» язык, не имеющий объективного содержания. Но такое истолкование базируется на рассмотрении «языка Т.» в духе классич. формализма как чисто знаковой формализованной системы, выра­жения к-рой могут получать познават. значение только путем эмпирич. интерпретации. Ограниченность такого подхода была доказана в ходе развития логики и метаматематики. Неудачу потерпели и попытки пост­роить «язык наблюдения» как формальный аналог «языка Т.».

Иной подход к проблеме «Т.— опыт» основан на от­казе от предположения о существовании особого «язы­ка наблюдения». В этом случае данные наблюдения, экспериментальные данные и т. п. должны быть сфор­мулированы на к.-л. ином языке и либо включаются в Т. в качестве выводимых в ней следствий, либо служат дополнит, исходными утверждениями. Проблема уста­новления познават. значения терминов «Т.» уподобляет­ся т. о. проблеме перевода их на нек-рый «понятный» язык.

Важно отметить, что теоретич. объекты неопределимы средствами данной Т.; постулаты об их существовании и наиболее существ, свойствах принадлежат к внетео-ретич. средствам. При определении смысла терминов, обозначающих индивидные объекты Т., иногда счи­тают, что этот смысл полностью задается правилами употребления терминов. Однако это слишком сильное допущение.Практически смысл таких терминов за­дается путем наложения нек-рых ограничений на ин­туицию (напр., при характеристике материальной точ­ки в механике ей «отказывают» в свойстве протяжен­ности). Постулирование нек-рых особых свойств инди­видов в Т. принадлежит к тем «онтологич. гипотезам», к-рые принимаются при построении каждой Т. (хотя обычно существо этих гипотез становится ясным лишь в достаточно зрелой Т.) и, более широко, во всяком неловеч. мышлении.

Проблема истинности или ложности утверждения внутри Т. эквивалентна проблеме его доказуемости или опровержимости; исключение может быть сделано для утверждений, недоказуемых и неопровержимых в Т., несмотря на их содержат, истинность; но для таких утверждений надо искать доказательства в более бога­тых системах, чтобы принимать их в качестве гипотез. Что же касается Т. в целом, то она как таковая ничего не говорит о своей истинности; Т. истинна, если она обладает предсказат. силой, а установление этого обс­тоятельства — дело не самой Т., а практики-

Анализ логич. структуры Т. и проводимые в послед­
ние годы исследования процесса построения Т. еще
раз показали, что нельзя создать «логику открытий»,
приводящую к автоматич. построению Т. Поэтому гл.
задача логич. анализа Т. состоит в выработке логич.
стандартов теоретич. знания, реализуемых затем в
конкретных науках. При этом наряду с анализом «го­
тового» знания логика переходит к изучению гене­
зиса знания и путей его использования, т. е. наряду
с логикой Т. исследуется и логика развития Т.: ус­
ловия выдвижения определ. системы абстракций (он­
тологич. гипотез), составляющих основание Т. и оп­
ределяющих ее эвристич. возможности и границы;
факторы, вызывающие необходимость фундаменталь­
ной перестройки осн. понятий и даже логич. принци­
пов Т.; причины и условия «миграций» отд.положений
и компонентов отвергнутой или устаревшей Т. в но­
вых системах знания и т.д.....^

Лит.: Маркс К., Капитал, в кн.: Маркс "К. и 9 н-г е л ь с Ф., Соч., 2 изд., т. 23—26; Ленин В. Й., Филос. тетради, Соч., 4 изд., т. 38; Гуссерль Э., Логич. исследования, СПБ, 1909; Кузнецов И. В., Принцип соответствия в совр. физике и его филос. значение, М.— Л., 1948; его же, Структура физич. теории, «ВФ», 1967,

Л¹» 11; Тарски й А., Введение в логику и методологию дедуктивных наук, пер. с англ., М., 1948; Вит­генштейн Л., Логико-филос. трактат, пер. с нем., М., 1958; Парная Р., Значение и необходимость, пер. с англ., М., 1959; Франк Ф., Философия науки, пер. с англ., М., 1960; Г р у ш и н Б. А., Очерки логики историч. исследования, М., 1961; К о т а р б и н ь с к и й Т., Избр. произв., пер. с польск., М., 1963; Садовский В. Н., Проблемы методологии дедуктивных теорий, «ВФ», 1963, Л"₈ 3; Проблемы логики науч. познания, М., 1964; Логика науч. исследования, М., 1965; Ракитов А. И., Логич. структура науч. теории, «ВФ», 1966, Л"» 1; Л я п,у нов А. А., О нек-рых особенностях строения совр. теоретич. знания, «ВФ», 1966, № 5; П о п о в и ч М. В., О филос. анализе языка науки, К., 1966; Ш в ы р е в В. С, Неопозитивизм и проблемы эмпирич. обоснования науки, М., 1966; Зиновьев А. А., Основы ло­гич. теории науч. знаний, М., 1967; К о п н и н П. В., Логич. основы науки, К., 1968; Ледников Е. Е., Проблема конструктов в анализе науч. теорий. К., 1969; А у е г А., Language, truth and logic, L., 1936; Wittgenstein L., Philosophical investigations, Oxf., 1953; Russell В., Logic and knowledge. Essays 1901—1950. L., 1956; Ca г n a p K., The methodological character of theoretical concepts, в кн.: Min­nesota studies in the philosophy of science, v. 1, Minneapolis, 1956; Hemp el C. G-., The theoretician's dilemma, там же, v. 2, Minneapolis, 1958; Pap A., Semantics and necessary truth, New Haven, 1958; Popper K. R., Logic of scientific discovery, L., 1959; Braithwaithe К. В., Scientific explanation, N.Y., 1960; Bunge M. A., Scientific research, v. 1—2, В.—N.Y.—W., 1967.

M. Попович. Киев, В. Садовский. Москва.

ТЕОРИЯ ГРАФОВ — одна из ветвей топологии. Графом называют геометрии, схему, представляющую собой систему линий, связывающих какие-то заданные точки. Точки наз. вершинами, а связывающие их ли­нии — ребрами (или дугами). Все задачи Т. г. могут решаться как в графической, так и в матричной форме. В случае записи в матричной форме возмож­ность передачи сообщения из данной вершины в дру­гую обозначается единицей, а ее отсутствие — Щ'лем.

Зарождение Т. г. в 18 в. связано с математич. головоломками, но особенно сильный толчок ее раз­витию был дан в 19 в. и гл. обр. в 20 в., когда обнаружились возможности ее практич приложений: для расчета радиоэлектронных схем, решения т. и. транспортных задач и др. С 50-х гг. Т. г. все шире используется в социальной психологии и социологии.

В области Т. г. следует назвать работы Ф. Харари, Дж. Кемени, К. Фламента, Дж. Снелла, Дж. Френча, Р. Нормана, О. Оэзера, А. Бейвеласа, Р. Вейса и др. В СССР по Т. г. работают Ф. М. Бородкин и др.

Язык Т. г. хорошо приспособлен для анализа раз­ного рода структур и передачи состояний. В соответст­вии с этим можно выделить след. типы социологич. и социально-психологич. задач, решаемых с помощью Т. г.

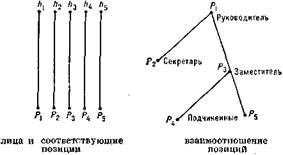
1) Формализация и построение общей структурной модели социального объекта на разных уровнях его сложности. Напр., структурная схема организации, социограммы, сравнение систем родства в разных обществах, анализ ролевой структуры групп и т. д. Можно считать, что ролевая структура включает три компонента: лица, позиции (в упрощенном варианте — должности) и задачи, выполняемые в данной позиции. Каждая компонента может быть представлена в виде графа*