Периодические сигналы могут быть описаны в виде суммы (или суперпозиции) гармонических составляющих или гармоник, каждая из которых имеет определённую частоту, амплитуду и начальную фазу. Конкретный набор таких составляющих будет определяться видом сигнала 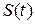 . Для того, чтобы такое представление можно было бы осуществить, фрагмент сигнала на периоде
. Для того, чтобы такое представление можно было бы осуществить, фрагмент сигнала на периоде 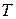 должен удовлетворять условиям Дирихле, т.е.:
должен удовлетворять условиям Дирихле, т.е.:
1) не должно быть разрывов II рода;
2) число разрывов I-го рода (или скачков) должно быть конечным;
3) число экстремумов должно быть конечным.
При соблюдении этих требований периодический сигнал 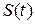 может быть представлен в виде ряда Фурье:
может быть представлен в виде ряда Фурье:
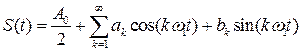 , (2.4)
, (2.4)
где 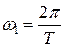 – круговая частота или период повторения сигнала;
– круговая частота или период повторения сигнала;
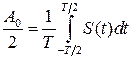 – постоянная составляющая сигнала;
– постоянная составляющая сигнала;
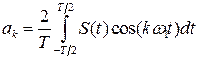 ;
;
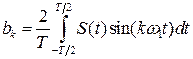 ;
;
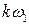 –
– 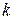 -я частотная составляющая сигнала или
-я частотная составляющая сигнала или 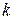 -я гармоника.
-я гармоника.
Заметим, что пределы интегрирования могут быть и другими, например, от 0 до 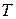 – важно, чтобы охватывался бы лишь весь период сигнала
– важно, чтобы охватывался бы лишь весь период сигнала 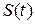 .
.
Если 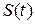 – чётная функция (это значит, что
– чётная функция (это значит, что 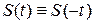 ), то все
), то все 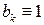 и, наоборот, если
и, наоборот, если 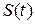 – нечётная функция (
– нечётная функция (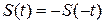 ), то все
), то все 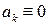 .
.
Такое разложение можно записать в тригонометрической форме:
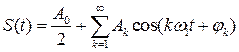 , (2.5)
, (2.5)
где 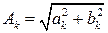 – амплитуда
– амплитуда 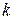 -й гармоники;
-й гармоники;
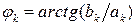 – начальная фаза.
– начальная фаза.
При этом если 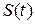 – чётная, то
– чётная, то 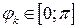 и если
и если 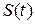 – нечётная, то
– нечётная, то 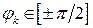 .
.
Множество амплитуд гармоники называют амплитудным спектром, а множество фаз – фазовым спектром.
Если 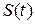 – действительная функция, то:
– действительная функция, то:
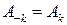
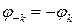 .
.
Пример: Пусть исходный сигнал представляет собой последовательность прямоугольных импульсов с постоянным периодом Т (рис. 2.1).
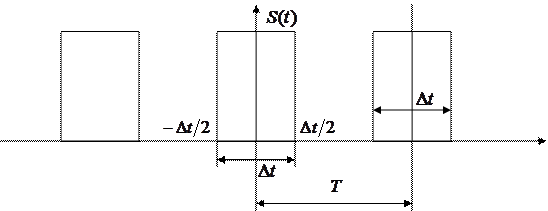 |
Рис.2.1. Последовательность прямоугольных импульсов
Т.к. такой сигнал чётный, то надо определить
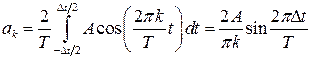
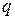 – скважность;
– скважность; 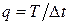 ;
;
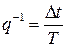 – коэффициент заполнения (duty cycle);
– коэффициент заполнения (duty cycle);
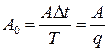
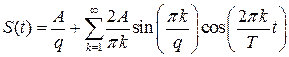
Амплитудный спектр подобного сигнала показан на рис.2.2..
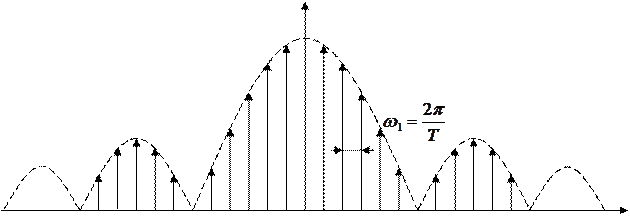 |
Рис.2.2. Амплитудный спектр последовательности прямоугольных импульсов.
Амплитудный и фазовый спектры периодических сигналов дискретны, т.е. определены на фиксированных частотах 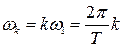
 2015-05-06
2015-05-06 895
895








