2015-05-06
442
Для одномерного случая прямое преобразование Хартли может быть определено как [3]
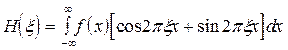(2.18)
и, соответственно, обратное преобра-зование Хартли
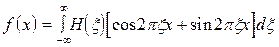(2.19)
Сравним эти выражения с (2.6.) и (2.9), разложив ядро по формуле Эйлера на действительную и мнимую части (т.е. sin и cos компоненты):
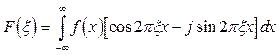(2.20)
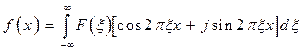
Из анализа (2.18) - (2.20), можно сделать следующие выводы:
1) Преобразование Хартли является преобразованием с действительным ядром;
2) Прямое и обратное преобразование Хартли вычисляются идентично;
3) Квадрат модуля преобразования Фурье | F(n) |2 равен:
 |
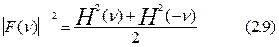4) Действительная и мнимая компоненты преобразования Фурье могут быть вычислены на основе преобразования Хартли весьма простым образом:
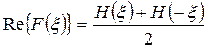(2.22)
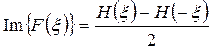(2.23)
5) Если f(x) - четная (т.е. f(-x)=f(x)), то:
, 
.
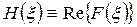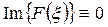Основные свойства преобразования Хартли соответствуют преобразованию Фурье:
1) Инвариантность к сдвигу (модуль H2(ξ) + H2(ξ) - неизменен).
2) Так же, как и для преобразования Фурье, для преобразования Хартли справедливы следующие соотношения согласно теоремы масштабов:
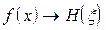
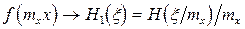
3) Так же, как и для преобразования Фурье, для преобразования Хартли справедлива Теорема Парсеваля.
Отличие от Фурье - преобразования заключается в иной трактовке теоремы о свертке:
Если заданы функции f(x) и g(x), причем H(ξ) и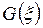 
- соответственно их cпектры Хартли:
,
,
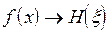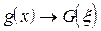то их свертка вычисляется следующим образом [3]:
1) вычисляются функци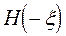и 
и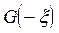 
;
2) формируется функция:
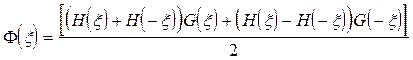
3) вычисляется преобразование Хартли от функции Ф(ξ).
Очевидно, что если функция g(x) - четная, то:
,
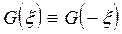
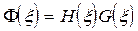Если и функция f(x) - четная, то:
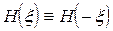
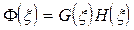
Преобразование Хартли требует вычислений примерно вдвое меньшей сложности (поскольку его ядро действительная функция) и в то же время от его результата достаточно просто перейти к результату, эквивалентному результату преобразования Фурье. Поэтому на практике преобразование Хартли используется вместо преобразования Фурье в различных задачах ЦОС как некоторое искусственное синтетическое преобразование меньшей сложности, но обеспечивающее получение требуемого результата.
