2015-05-06
383
1. Линейность:
если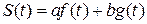 
то:
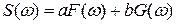. ( 2.10 )
2. Инвариантность к линейному смещению (задержке) сигнала:
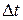– время задержки:
; 
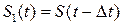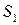– задержанная на 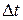копия сигнала 
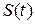, тогда:
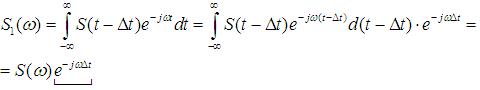(2.11)
линейный фазовый множитель.
Отсюда следует, что амплитудный спектр сигнала не изменится при любой его задержке (линейный сдвиг). Фазовый спектр приобретает дополнительное слагаемое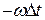 
, линейно зависящее от частоты.
3. Масштабируемость спектральной плотности
Пусть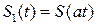 
, где 
– масштабирующий множитель, при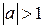 
сигнал сжимается, при 
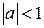– растягивается, кроме того если 
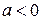, то дополнительно происходит зеркальное отражение сигнала по вертикальной оси.
Для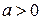 
:
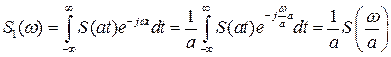
Для :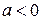
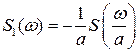(2.12)
или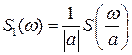 
; 
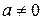
И для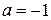 
:
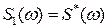
4. Дифференцирование сигнала:
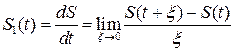
Тогда
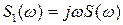(2.13)
При дифференцировании низкие частоты ослабляются, а высокие усиливаются. Фазовый спектр сдвигается на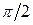 
для положительных частот и на 
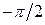– для отрицательных.
5. Интегрирование сигнала
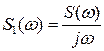– это справедливо для сигналов, не содержащих постоянных составляющих, т.е. если 
.
В противном случае появляется дополнительное слагаемое от постоянной составляющей в виде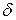 
- функции на частоте 
.
|
|
|
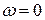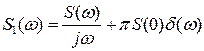(2.14)
При этом происходит ослабление высоких частот и усиление низкочастотных гармоник.
6. Спектр свёртки двух сигналов:
Свёртка двух сигналов определяется как:
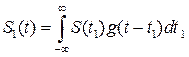, тогда спектральная плотность свёртки двух сигналов есть:
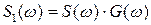(2.15)
7. Спектральная плотность от произведения двух сигналов
Пусть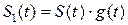 
Тогда спектральная плотность такого сигнала равна:
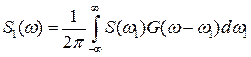, (2.16)
т.е. является свёрткой спектральных плотностей двух сигналов.
8. Эффект переноса спектра
Умножим исходный сигнал на гармоническую функцию:
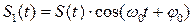
и попытаемся найти спектральную плотность такого сигнала:
.
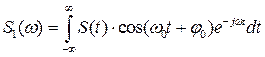Представим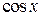 
в виде:
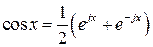– на основе формулы Эйлера, тогда:
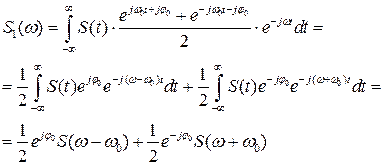(2.17)
9. Равенство Парсеваля или закон сохранения энергии:
.
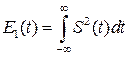
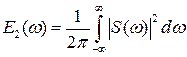
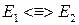Однако на практике сигнал имеет конечную длительность, т.е. финитен:
тогда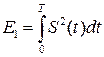 
– и является определённым интегралом, т.е. числом.
Величина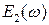 
является определённым интегралом
тогда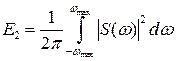 
– также является определённым интегралом
и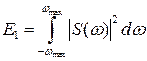 
.
Под практической полосой частот сигнала понимается полоса частот, в пределах которой передаётся подавляющая доля энергии сигнала (до 90÷95).
Тогда:
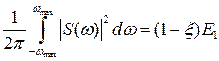
Ширина полосы частот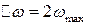 
называется практической шириной спектра сигнала.
