2015-05-06
3186
Рассмотрим сигнал, у которого одновременно осуществляется по какому-либо закону изменение (модуляция) амплитуды и фазы:
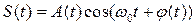(2.6)
В (2.6)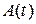 
называют амплитудой огибающей; 
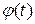– фазовой функцией сигнала 
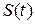. Полная фаза сигнала 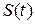определяется как:
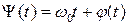
Сигнал вида (2.6) можно представить как вещественную часть импульсной функции:
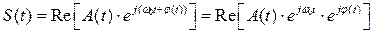(2.7)
В (2.7)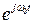 
определяет собой несущий немодулированный гармонический сигнал, множител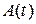и и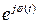 
несут информацию об амплитудной огибающей и фазовой функции сигнала. Их произведение называют комплексной огибающей сигнала:
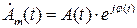. (2.8)
Для отличия того, что эта функция комплексная, обозначим её с точкой.
Введём понятие комплексного сигнала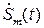 
(иногда его называют аналитическим сигналом).
Произвольный сигнал 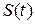представляет собой действительную (вещественную) часть сигнала .
.
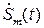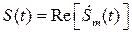Для того, чтобы было возможным определить как амплитуду, так и фазу сигнала, необходима мнимая часть исходного комплексного сигнала:
,
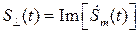которая называется сопряжённым сигналом или квадратурным дополнением.
|
|
|
Тогда:
.
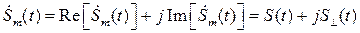Квадратурное дополнение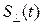 
можно получить из 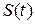с помощью преобразования Гильберта, которое имеет вид:
.
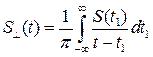Точно также, с помощью обратного преобразования Гильберта может быть по 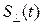получен сигнал :
.
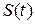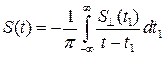4. ПЕРЕХОД ОТ АНАЛОГОВЫХ СИГНАЛОВ К ЦИФРОВЫМ
Переход от непрерывных аналоговых сигналов к цифровым осуществляется с помощью процедур дискретизации и квантования, выполняемых последовательно друг за другом. Их совместное применение называют аналого-цифровым преобразованием.
Процесс перехода от непрерывной области изменения аргумента (задания функции) к конечному множеству отдельных значений аргумента называется дискретизацией.
Процесс перехода от непрерывной области изменения функции к конечному множеству определенных значений называется квантованием.
