1.НТ1(З). Если l – пройденный телом между двумя точками, а 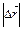 - модуль соответствующего перемещения, то
- модуль соответствующего перемещения, то
А) 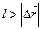 ;
;
В) 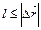 ;
;
*С) 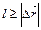 ;
;
Д) 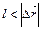 .
.
2.НТ1(З). Если 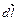 – бесконечно малый направленный отрезок пути материальной точки, а
– бесконечно малый направленный отрезок пути материальной точки, а 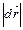 - вектор соответствующего элементарного перемещения, то
- вектор соответствующего элементарного перемещения, то
А) 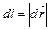 ;
;
В) 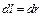 , где dr – изменение длины радиуса-вектора
, где dr – изменение длины радиуса-вектора 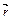 в результате элементарного перемещения;
в результате элементарного перемещения;
*С) 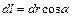 , где da - угол между
, где da - угол между 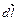 и
и 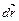 ;
;
Д) 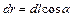 .
.
3.НТ1(О). Направленный отрезок прямой, соединяющий на траектории две любые точки 1 и 2, в которые попадает материальная точка в моменты времени t 1 и t 2, называют вектором……
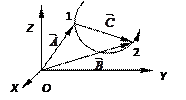 Ответ: перемещения.
Ответ: перемещения.
4.НТ1(О). На рисунке представлена траектория материальной точки. Вектор перемещения м.т. из 1 в 2 это вектор….
Ответ: С
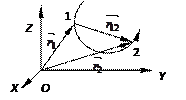 5.НТ1(З). На рисунке представлена траектория материальной точки. Если
5.НТ1(З). На рисунке представлена траектория материальной точки. Если 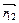 - вектор перемещения тела из точки с радиусом-вектором
- вектор перемещения тела из точки с радиусом-вектором 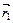 в точку с радиусом-вектором
в точку с радиусом-вектором 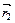 , то
, то
А) 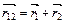 ;
;
В) 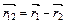 ;
;
*С) 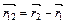 ;
;
Д) 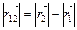 .
.
6.НТ1(З). Верным утверждением о модулях мгновенной, средней по перемещению и среднепутевой скоростей является
А) всегда не равны друг другу;
*В) одинаковы при стремлении времени наблюдения за перемещением к нулю;
С) при стремлении времени наблюдения к нулю всегда одинаковы только модули мгновенной и средней по перемещению скоростей;
Д) всегда равны модули средней по перемещению и среднепутевой скорости.
7.НТ1(О). Число степеней свободы системы, состоящей из N = 30 материальных точек, равно: i = ….
Ответ: 90
8.НТ1(О). Число степеней свободы системы, состоящей из двух материальных точек, связанных между собой невесомым нерастяжимым стержнем (двухатомная молекула), равно: i = ….
Ответ: 5
9.НТ1(О). Число степеней свободы системы, состоящей из трех материальных точек, жестко связанных между собой невесомыми нерастяжимыми стержнями (трехатомная молекула), равно: i = ….
Ответ: 6
10.НТ1(О). Число степеней свободы «абсолютно» твердого тела равно: i = ….
Ответ: 6
11.НТ1(О). Число степеней свободы системы, состоящей из четырех материальных точек, жестко связанных между собой невесомыми нерастяжимыми стержнями (четырехатомная молекула), равно: i = ….
Ответ: 6
12.НТ1(О). Число колебательных степеней свободы двухатомной молекулы равно: iк = ….
Ответ: 5
13.НТ2(О). Число колебательных степеней свободы трехатомной молекулы равно: iк = ….
Ответ: 3
14.НТ2(О). Камень брошен под углом к горизонту со скоростью 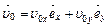 . Запишите формулу для модуля нормального ускорения в момент броска, используя шаблон: cb @ db @ cd, где
. Запишите формулу для модуля нормального ускорения в момент броска, используя шаблон: cb @ db @ cd, где
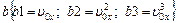 ;
;
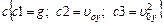 ;
;
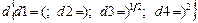 ;
;
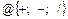
Ответ: c 1 b 1/ d 1 b 2+ c 3 d 3 или c1b1/d1b2+c3d3
15.НТ2(О). Движение материальной точки описывается уравнениями: 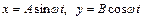 . Запишите уравнение траектории в явной форме, используя шаблон: a @ b @ a @ b @ c
. Запишите уравнение траектории в явной форме, используя шаблон: a @ b @ a @ b @ c
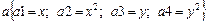 ;
;
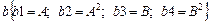 ;
;
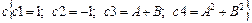 ;
;
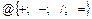
Ответ: a 2/ b 2+ a 4/ b 4= c 1 илиa2/b2+a4/b4=c1
16.НТ1(О). Камень брошен горизонтально с горы со скоростью 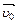 . Запишите уравнение траектории в явном виде (y = y (x)), используя шаблон: a @ ba @ dbbd
. Запишите уравнение траектории в явном виде (y = y (x)), используя шаблон: a @ ba @ dbbd
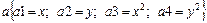 ;
;
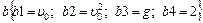 ;
;
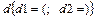 ;
;
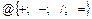
Ответ: a 2= b 3 a 3/ d 1 b 4 b 2 d 2 или a2=b3a3/d1b4b2d2
17.НТ2(З). Тангенциальная составляющая ускорения материальной точки 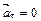 , а нормальная составляющая
, а нормальная составляющая
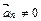 . В этих условиях траектория точки:
. В этих условиях траектория точки:
А) всегда окружность;
В) окружность или винтовая линия;
С) обязательно кривая линия, которая только при 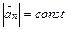 будет винтовой линией или окружностью;
будет винтовой линией или окружностью;
*Д) обязательно кривая линия, которая только при 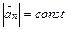 и вектором
и вектором 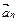 , параллельным одной плоскости, будет винтовой линией или окружностью.
, параллельным одной плоскости, будет винтовой линией или окружностью.
18.НТ1(З). Если касательное ускорение материальной точки 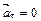 , то ее траектория будет окружностью
, то ее траектория будет окружностью
А) если модуль нормального ускорения 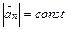 ;
;
В) если модуль нормального ускорения 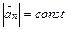 , и вектор
, и вектор 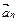 параллелен одной плоскости;
параллелен одной плоскости;
*С) если модуль нормального ускорения 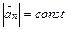 , и вектор
, и вектор 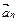 параллелен одной плоскости, а компонента скорости. перпендикулярная этой плоскости, равна нулю;
параллелен одной плоскости, а компонента скорости. перпендикулярная этой плоскости, равна нулю;
Д) всегда.
19.НТ2(З). Если материальная точка движется по окружности и касательное ускорение 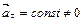 , то модуль нормального ускорения
, то модуль нормального ускорения
А) увеличивается пропорционально 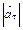 ;
;
В) пропорционально 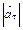 увеличивается или уменьшается в зависимости от знака проекции
увеличивается или уменьшается в зависимости от знака проекции 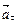 на направление скорости;
на направление скорости;
*С) изменяется пропорционально 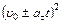 ;
;
Д) не зависит от 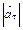 , так как an определяется центростремительной силой.
, так как an определяется центростремительной силой.
20.НТ1(О).  Установите связь между координатами точки М в прямоугольной М (x, y, z) и сферической М (r, q, j) системах координат:
Установите связь между координатами точки М в прямоугольной М (x, y, z) и сферической М (r, q, j) системах координат:
х = …;
y = …;
z = ….
Ответ: x = rsinqcosj
y = rsinqsinj
z = rcosq
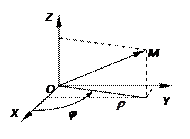 21.НТ1(О). Установите связь между координатами точки М в прямоугольной М (x, y, z) и цилиндрической М (r, q, z) системах координат:
21.НТ1(О). Установите связь между координатами точки М в прямоугольной М (x, y, z) и цилиндрической М (r, q, z) системах координат:
х = …;
y = …;
z = ….
Ответ: x = r cos j
y = r sin j
z = z
22.НТ1(О). При движении материальной точки приращение ее радиус-вектора за промежуток времени D t - это вектор …..
Ответ: перемещения.
23.НТ1(З). Векторное произведение 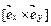 равно
равно
А) 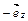 ;
;
*В) 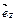 ;
;
С) 0;
Д) 1.
24.НТ1(З). Векторное произведение 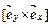 равно
равно
*А) 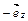 ;
;
В) 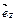 ;
;
С) 0;
Д) 1.
25.НТ1(З). Скалярное произведение 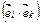 , где i, k – x, y, z, равно
, где i, k – x, y, z, равно
А) 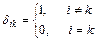 ;
;
В) 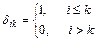 ;
;
*С) 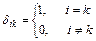 ;
;
Д) 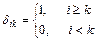 .
.
26.НТ1(З). Скалярное произведение вектора скорости 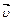 на нормаль
на нормаль 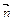 к траектории
к траектории 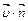 равно
равно
А) u cos a, где a - угол между направлением вектора скорости и радиусом-вектором;
В) - u cos a, где a - угол между направлением вектора скорости и радиусом-вектором;
С) - u cos b, где b - угол между направлением вектора нормали к траектории и радиусом-вектором;
*Д) 0.
27.НТ1(З). За время D t 12 = t 1 - t 2 материальная точка прошла путь l 12 в начале и в конце которого радиус-вектор изменился на 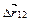 . Отношение модулей средней скорости перемещения к средней путевой скорости равно:
. Отношение модулей средней скорости перемещения к средней путевой скорости равно:
А) 1 всегда;
В) 1 при прямолинейном движении и больше 1 при любом другом;
С) 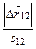 ;
;
Д) 1 при прямолинейном движении и меньше 1 при любом другом.
Неверные ответы: А, В
28.НТ2(О). Запишите формулу для вектора полного ускорения (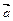 ) при произвольном движении материальной точки, используя для этого шаблон:
) при произвольном движении материальной точки, используя для этого шаблон: 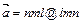
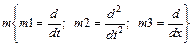 ;
;
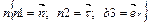 ;
;
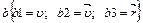 ;
;
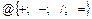
Ответ: n 2 m 1 b 1+b1 m 1 n 2 или n2m1b1+b1m1n2
29.НТ1(З). Если 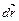 - вектор элементарного перемещения, а
- вектор элементарного перемещения, а 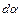 - угол между касательными прямыми, проведенными к траектории в точках начала и конца
- угол между касательными прямыми, проведенными к траектории в точках начала и конца 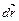 , то радиус R кривизны траектории
, то радиус R кривизны траектории
*А) 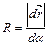 ;
;
В) 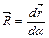 ;
;
С) по приведенным данным определить нельзя, так как угол 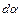 не связан с R;
не связан с R;
Д) равен 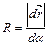 только если начало координат совпадает с центром кривизны.
только если начало координат совпадает с центром кривизны.
30.НТ2(О). Запишите формулу для вектора полного ускорения (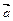 ) при произвольном движении материальной точки, используя для этого шаблон:
) при произвольном движении материальной точки, используя для этого шаблон: 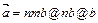
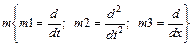 ;
;
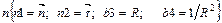 ;
;
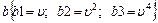 ;
;
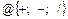
Ответ: n 2 m 1 b 1+n1 b 2 /b 3 или n2m1b1+n1b2/b3
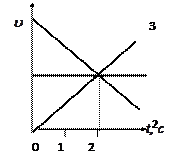
31.НТ1(З). На рисунке представлены графики зависимости от времени модулей скорости трех тел. Верное соотношение пройденных телами путей за 2 с:
*A) s1>s2>s3;
B) s1<s2<s3;
C) s1=s2=s3;
D) s1<s2>s3;
32.НТ1(З). Санки начинают скатываться с горки, длина которой l. Ускорение санок постоянно и равно a. Формула для расчета времени скатывания санок до середины горки имеет вид:
A) 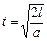 ;
;
*B) 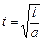 ;
;
C) 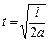 ;
;
Д) 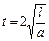
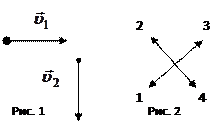
33.НТ1(О). Один автомобиль приближается к перекрестку со скоростью 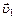 , а другой – удаляется со скоростью
, а другой – удаляется со скоростью 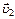 (рис. 1). Направление вектора скорости движения второго автомобиля относительно первого указано на рис.2 под номером ….
(рис. 1). Направление вектора скорости движения второго автомобиля относительно первого указано на рис.2 под номером ….
Ответ: 1
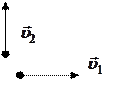 34.НТ1(З). Два автомобиля движутся со скоростями
34.НТ1(З). Два автомобиля движутся со скоростями 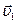 и
и 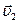 в системе отсчета, связанной с Землей. Модуль скорости первого автомобиля относительно второго равен:
в системе отсчета, связанной с Землей. Модуль скорости первого автомобиля относительно второго равен:
A) 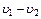 ;
;
B) 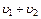 ;
;
*C) 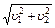 ;
;
Д) 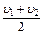 .
.
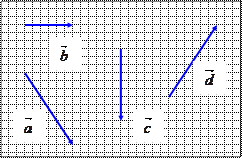
35.НТ1(З). На рисунке представлены четыре вектора перемещения. Из приведенных ниже для этих векторов не выполняется соотношение:
A) 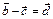 ;
;
B) 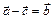 ;
;
*C) 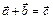 ;
;
Д) 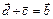 .
.
36.НТ1(О). Запишите в векторной форме формулу для вектора скорости материальной точки, если движение вдоль оси ОХ происходит с постоянной скоростью 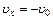 , вдоль оси OZ с ускорением
, вдоль оси OZ с ускорением 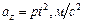 при начальной проекции скорости
при начальной проекции скорости 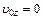 , и вдоль оси OY
, и вдоль оси OY 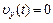 . Для записи используйте шаблон:
. Для записи используйте шаблон: 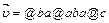 .
.
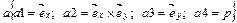 ;
;
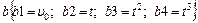 ;
;
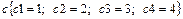
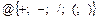
Ответ: - b 1 a 1+ a 4 b 4 a 2/ c 3 или -b1a1+a4b4a2/c3
37.НТ1(О). Радиус-вектор материальной точки меняется со временем по закону 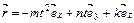 . Запишите формулу для вектора скорости точки, используя шаблон:
. Запишите формулу для вектора скорости точки, используя шаблон: 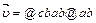 .
.
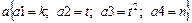 ;
;
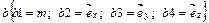 ;
;
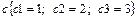
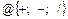
Ответ: - c 2 b 1 a 2 b 2+ a 1 b 3 или -c2b1a2b2+a1b3
38.НТ1(З). Движение произвольных элементов (точек) твердого тела представлять как движение одной из его точек и вращения остальных относительно этой, выбранной произвольно точки
*A) можно всегда;
B) можно только если выбранная точка является центром масс;
C) в общем случае нельзя, так как разные элементы будут двигаться с неодинаковыми по модулю и направлению скоростями;
Д) можно представлять только в случае плоскопараллельного движения.
39.НТ1(О). При вращении твердого тела вокруг неподвижной оси связь между линейной скоростью (u) произвольной точки тела, угловой скоростью (w) и расстоянием (r) точки до оси имеет вид…. Для записи формулы используйте шаблон: a @ a @ b.
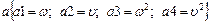 ;
;
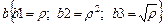 ;
;
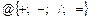
Ответ: a 1= a 2/ b 1 или a1=a2/b1
40.НТ1(О). Утверждение: любое конечное положение твердого тела можно получить из начального положения одним поворотом вокруг неподвижной точки, называют теоремой ….
Ответ: Эйлера.
41.НТ1(О). Запишите формулу, связывающую между собой линейную скорость (u) некоторой точки твердого тела, угол (dj) элементарного поворота тела, время (dt), за которое произошел элементарный поворот и расстояние (r) до мгновенной оси вращения. Для записи формулы используйте шаблон: a @ ba @ b.
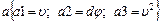 ;
;
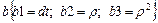 ;
;
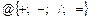
Ответ: a 1= b 2 a 2/ b 1 или a1=b2a2/b1
42.НТ1(О). Запишите формулу, для мгновенного значения нормального ускорения одной из точек твердого тела вращающегося вокруг неподвижной точки, используя шаблон: an = cb @ c.
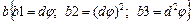 ;
;
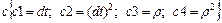 ;
;
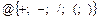
Ответ: c 3 b 2/ c 2 или c3b2/c2
43.НТ1(З). Если в некоторый момент времени t вектор угловой скорости относительно начала координат равен 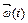 , то вектор линейной скорости материальной точки в этот момент равен:
, то вектор линейной скорости материальной точки в этот момент равен:
A) 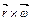 ;
;
*B) 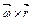 ;
;
C) 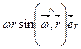 ;
;
Д) 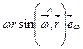 .
.
44.НТ1(З). Вектор углового ускорения 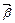 направлен
направлен
A) всегда параллельно 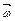 ;
;
B) всегда параллельно или антипараллельно 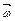 ;
;
C) либо параллельно или антипараллельно 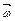 , либо сонаправлен с
, либо сонаправлен с 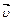 ;
;
*Д) произвольным образом относительно 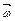 .
.
45.НТ1(З). При поступательно вращательном движении вектор углового ускорения 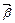
A) может иметь произвольное направление;
*B) параллелен или антипараллелен 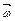 ;
;
C) всегда совпадает с направлением оси OZ неподвижной системы отсчета координат тела;
Д) не имеет направления, а 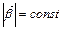 .
.
 2015-05-06
2015-05-06 3527
3527







