Для выражения абсолютной скорости роста (снижения) уровня ряда динамики исчисляют статистический показатель – абсолютный прирост (Δ). Его величина определяется как разность двух сравниваемых уровней. Она вычисляется по формуле
цепной - 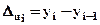 или
или
базисный - 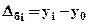 ,
,
где 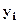 ‑ уровень i - го года;
‑ уровень i - го года;
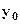 ‑ уровень базисного года.
‑ уровень базисного года.
Интенсивность изменения уровней ряда динамики оценивается отношением текущего уровня к предыдущему или базисному, которое всегда представляет собой положительное число. Этот показатель принято называть темпом роста (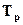 ). Он выражается в процентах, т.е.
). Он выражается в процентах, т.е.
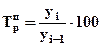 или
или 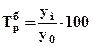 .
.
Для выражения изменения величины абсолютного прироста уровней ряда динамики в относительных величинах определяется темп прироста (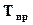 ). Который рассчитывается как отношение абсолютного прироста к предыдущему или базисному уровню, т.е.
). Который рассчитывается как отношение абсолютного прироста к предыдущему или базисному уровню, т.е.
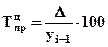 или
или 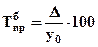 .
.
Показатель абсолютного значения одного процента прироста (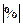 ) определяется как результат деления абсолютного прироста на соответствующий темп прироста, выраженный в процентах, т.е.
) определяется как результат деления абсолютного прироста на соответствующий темп прироста, выраженный в процентах, т.е.
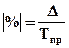 или
или 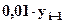 .
.
Расчет этого показателя имеет смысл только на цепной основе.
В интервальном ряду динамики с равностоящими уровнями во времени расчет среднего уровня ряда (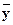 ) будет производиться по формуле средней арифметической простой:
) будет производиться по формуле средней арифметической простой:
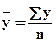 .
.
Определение среднего абсолютного прироста производится по цепным абсолютным приростам по формуле:
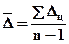 или
или 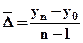
Среднегодовой темп роста:
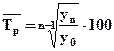 ,
,
Среднегодовой темп прироста:
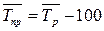
Среднее абсолютное значение 1% прироста можно рассчитать по формуле:
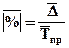
Задание 1. По данным таблицы рассчитайте цепные, базисные и средние:
а) абсолютные приросты;
б) темпы роста;
в) темпы прироста.
Таблица – Динамика продажи мясных консервов в одном из регионов за 2004-2008 гг. и расчет аналитических показателей динамики (данные условные).
| Годы | Консервы мясные, млн.усл.банок | Абсолютные приросты (снижение), млн.усл.банок | Темпы роста, % | Темпы прироста, % | Абсолютное значение 1% прироста, млн.усл.банок | |||
Δ 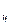
| Δ 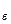
| Т 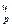 · ·
| Т 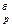
| Т 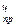
| Т 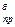
| |||
| Итого |
Суть метода скользящей средней состоит в замене абсолютных данных средними арифметическими за определенные периоды. Расчет средних ведется способом скольжения, т.е. постепенным исключением из принятого периода скольжения первого уровня и включением следующего.
Задание 2. По данным таблицы произведите сглаживание ряда динамики на основе 4-х уровневой скользящей средней. Постройте графики исходного и сглаженных рядов динамики.
Таблица – Динамика производства стиральных машин и расчет скользящих средних
| Месяцы | Стиральные машины, тыс.шт. | Четырехчленные скользящие суммы | Четырехчленные скользящие средние |
Наиболее эффективным способом выявления основной тенденции развития является аналитическое выравнивание. При этом уровни ряда динамики выражаются в виде функции времени:
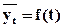
Для выравнивания ряда динамики по прямой (на основе линейной функции) используется уравнение:
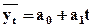
Способ наименьших квадратов дает систему двух нормальных уравнений для нахождения параметров a 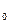 и a
и a 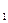 :
:

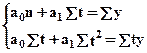
где y – исходный уровень ряда динамики;
n –число членов ряда;
t – показатель времени, который обозначается порядковыми номерами, начиная от низшего.
Решение системы уравнений позволяет получить выражения для параметров a 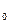 и a
и a 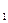 :
:
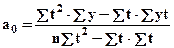 ;
;
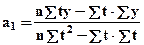 .
.
Основная тенденция (тренд) показывает, как воздействуют систематические факторы на уровень ряда динамики, а колеблемость уровней около тренда служит мерой воздействия остаточных факторов. Ее можно измерить по формуле:
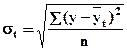 ‑ среднее квадратическое отклонение
‑ среднее квадратическое отклонение
Относительной мерой колеблемости является коэффициент вариации:
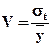 .
.
Задание 3. По данным таблицы произведите аналитическое выравнивание данного динамического ряда на основе линейной функции 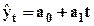 . Рассчитайте колеблемость уровней около тренда по формуле. Постройте графики исходного и сглаженных рядов динамики.
. Рассчитайте колеблемость уровней около тренда по формуле. Постройте графики исходного и сглаженных рядов динамики.
Таблица – Исходные данные для определения параметров системы уравнений о динамике производства молока в регионе 2003‑2008 гг..
| Годы | 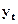
| t | t 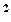
| t 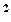 y y
| Расчет показателя колеблемости на основе линейной функции | ||
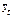
| 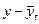
| 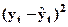
| |||||
| 13,3 | |||||||
| 13,5 | |||||||
| 14,8 | |||||||
| 16,1 | |||||||
| 16,6 | |||||||
| 17,3 | |||||||
| Итого |
При анализе ряда динамики важное значение имеет выявление сезонных колебаний. При изучении сезонных колебаний используются специальные показатели – индексы сезонности (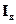 ).
).
Для ряда внутригодовой динамики, в которой основная тенденция роста незначительна (или она не наблюдается совсем), изучение сезонности основано на методе постоянной средней: являющейся средней из всех рассматриваемых уровней. Самый простой способ заключается в следующем: для каждого года рассчитывается средний уровень, а затем с ним сопоставляется (в процентах) уровень каждого месяца. Это процентное отношение обычно именуется индексом сезонности:
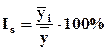 .
.
Задание 4. Рассчитайте индекс сезонности.
Таблица – Внутригрупповая динамика числа расторгнутых браков населения города по месяцам за 2006-2008 гг.
| Месяцы | Число расторгнутых браков | Индекс сезонности
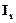
| |||
в среднем за 3 года
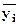
| |||||
Средний уровень ряда (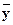 ) )
|
 2015-05-06
2015-05-06 1071
1071