Первая: Зная закон движения материальной точки массы m, найти равнодействующую всех сил 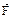 , действующих на точку в каждый данный момент.
, действующих на точку в каждый данный момент.
Движение точки задано координатным способом, т.е. 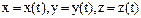 (1). Определив проекции ускорения из уравнений (1), запишем ДУ движения точки в проекциях на декартовы оси координат:
(1). Определив проекции ускорения из уравнений (1), запишем ДУ движения точки в проекциях на декартовы оси координат:
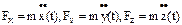 . Решение сводиться к двукратному дифференцированию закона движения точки. Определив три проекции силы
. Решение сводиться к двукратному дифференцированию закона движения точки. Определив три проекции силы 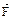 , мы будем знать ее модуль и направление в каждый момент времени t.
, мы будем знать ее модуль и направление в каждый момент времени t.
Вторая: По заданной силе 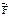 , действующей на материальную точку массы m, требуется определить закон движения точки. Сила
, действующей на материальную точку массы m, требуется определить закон движения точки. Сила 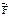 и ее проекции могут зависеть от координат, скорости и времени. Запишем ДУ движения точки:
и ее проекции могут зависеть от координат, скорости и времени. Запишем ДУ движения точки:

Решение сводиться к интегрированию системы трех ДУ второго порядка. Общее решение этой системы будет содержать 6 произвольных постоянных:
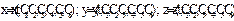
Константы найдём из начальных условий: 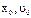 при
при 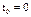 .
.
 2015-05-06
2015-05-06 571
571








