- Ф-ция 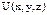 зависит только от координат, частные производные от этой ф-ции по координатам равны проекциям силы силового поля на соотв. оси:
зависит только от координат, частные производные от этой ф-ции по координатам равны проекциям силы силового поля на соотв. оси: 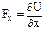 ;
; 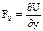 ;
; 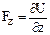 (1)
(1)
- Ф-ция 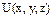 , удовл. условиям (1), наз. силовой функцией данного силового поля, а само силовое поле наз. пот. (консервативным).
, удовл. условиям (1), наз. силовой функцией данного силового поля, а само силовое поле наз. пот. (консервативным).
- Пот. энергией в данной точке пот. силового поля называется величина той работы, которую совершила бы сила поля при перемещ. материальной точки из данной точки поля в ту, в которой пот. энергия принанята равной нулю. 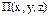 - пот. энергия. Пот. энергия характеризует запас энергии в данной точке поля.
- пот. энергия. Пот. энергия характеризует запас энергии в данной точке поля.
- Все силы, действ. на точки системы (внешние и внутренние) пот., то есть сущ. такая ф-ция 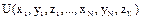 , что
, что 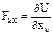 ;
; 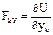 ;
; 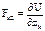 (
(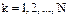 ).
).
Теорема о кинетической энергии для системы: 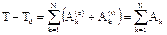 .
.
Если система движется в пот. поле, то: 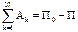 .
.
П - пот. энергия всех внешних и внутренних сил, действующих на систему.
Следовательно: 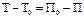 или
или 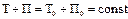
Сумма Т и П энергии системы называется полной механической энергией E: 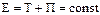 .
.
 2015-05-06
2015-05-06 543
543








