2015-05-06
681
Применим принцип Даламбера к каждой точке системы, получим N векторных уравнений:
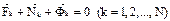или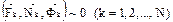 
.
Сложим почленно все уравнения: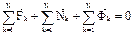 
. Перепишем: 
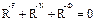(1).
При движении механической системы в любой момент времени сумма главных векторов активных сил, реакций связей и сил инерции равна нулю.
О - произвольный центр, проведем из него к каждой точек радиус-вектор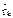 
:
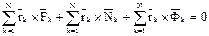. Перепишем: 
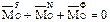(2).
В каждый момент времени сумма главных моментов активных сил, реакций связей и сил инерции движущейся механической системы, относительно некоторого центра О равна нулю.
При нахождени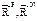и 
и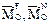 
учитываем только внешние силы, так как главный вектор и главный момент внутренних сил равны нулю.
В проекциях на оси координат, векторные условия (1) и (2) принимают вид ур-ний равновесия произвольной пространственной механической системы сил:
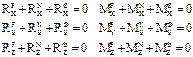Движение механической системы полностью опр. этими шестью уравнениями кинетостатики.
