2015-05-06
234
Для равновесия механической системы, на которую наложены голономные, стационарные, удерживающие и идеальные связи, необходимо и достаточно, чтобы сумма работ всех активных сил, приложенных к точкам системы, на любом возможном перемещении системы равнялась нулю.
Доказательство необходимости:
Система мат. точек, удовл. принципу возможных перемещений, наход. в равновесии. Докажем, что выполн. равенство: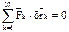 
. Если система в равновесии => любая точка системы в равновесии. Сумма активных сил 
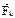и реакций связи 
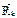, прилож. к каждой точке системы, должна быть равна нулю: 
, 
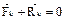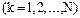. Из этого следует, что и работа этих сил на любом возможном перемещении 
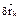также равна нулю: 
, 
.
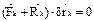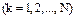Просуммирует по k и раскроем скобки: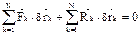 
. 
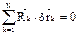в силу идеальности связей => 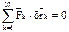. *необходимость доказана*
