2015-05-06
207
Для равновесия механической системы, на которую наложены голономные, стационарные, удерживающие и идеальные связи, необходимо и достаточно, чтобы сумма работ всех активных сил, приложенных к точкам системы, на любом возможном перемещении системы равнялась нулю.
Доказательство достаточности:
Выполняется равенство 
(1). Докажем, что система находиться в равновесии.
От противного: (1) выполняется, но система в равновесии не находиться. Это означает, что система под действием активных сил и сил реакций за малый промежуток времени совершит некоторое действ. перемещ. На этом действ. перемещ.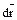 
равнодействующая сил 
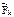и 
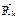совершит работу, отличную от нуля. Так как система находилась в покое, направл. действ. перемещ. совпадет с направл. равнодействующей сил 
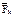и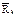 
=> работа будет положительной: 
, 
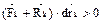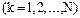. Просуммируем по k и раскроем скобки: 
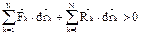(2). В случае стационарных связей действ. перемещ. совпадают с одним из возможных, то есть 
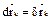. Из (2) получим: 
. 
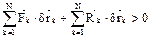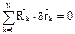в силу идеальности связей => 
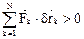, что противоречит условию (1). *достаточность доказана*
