Запишем выражение для возможных работ всех сил, прилож. к точкам системы, через обобщ. коорд.:
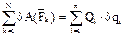 , тут
, тут 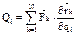 .
.
Обобщ. силой, соотв. некоторой обобщ. координате, называется скалярная величина, равная коэффициенту при вариации этой обобщ. координаты 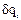 в выражении возможной работы всех активных сил, действ. на механическую систему.
в выражении возможной работы всех активных сил, действ. на механическую систему.
Аналитический способ: 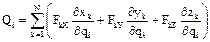 (1)
(1)
Система с числом степеней свободы >1:
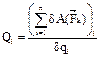 Системе можно сообщить такое возможное перемещ., при котором изменяется одна обобщ. координата
Системе можно сообщить такое возможное перемещ., при котором изменяется одна обобщ. координата 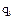 , соотв. искомой обобщ. силе
, соотв. искомой обобщ. силе 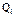 . Возможное перемещ. этой обобщ. координаты не равно нулю
. Возможное перемещ. этой обобщ. координаты не равно нулю 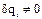 , а остальные
, а остальные 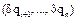 равны нулю.
равны нулю.
Индекс i означает, что возможная работа сил, соотв. вариации только i-ой обобщ. координате.
Силы потенциальные:
Пот. сила: 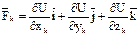 , подставим в (1):
, подставим в (1): 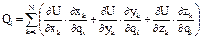 - частная производная силовой ф-ции
- частная производная силовой ф-ции 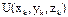 по i-ой обобщ. координате. Тогда:
по i-ой обобщ. координате. Тогда: 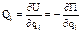 .
.
 2015-05-06
2015-05-06 242
242








