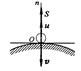
 Вектор скорости
Вектор скорости 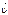 центра шара в начале удара совпадает с нормалью к поверхности в точке соударение - удар называется прямым.
центра шара в начале удара совпадает с нормалью к поверхности в точке соударение - удар называется прямым.
Шар до удара и после удара двигается поступат., считаем его материальной точкой массой m.
После удара шар имеет скорость 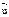 , направленную обратно по нормали.
, направленную обратно по нормали.
Перемещ. при ударе пренебрегаем => силой трения можно пренебречь, ударной силой является только нормальная реакция опоры 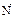 .
.
Теорема об изменении количества движения за время 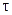 . Импульс ударной силы -
. Импульс ударной силы - 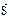 . Пренебрегаем действием неударной силы - силы тяжести:
. Пренебрегаем действием неударной силы - силы тяжести: 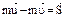 (1).
(1).
Проецируем (1) на нормаль: 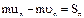 , учтем:
, учтем: 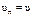 ,
, 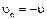 ,
, 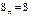 . Тогда:
. Тогда: 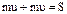 .
.
При прямом ударе шара о неподвижную поверхность величина, равная отношению абсолютных величин скорости в конце удара к скорости в начале удара, наз. коэфф. восстановления: 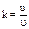 .
.
Коэфф. восст. не может быть >1 и в зависимости от материала соудар. тел принимает значения от 0 до 1.
1. k = 0, скорость поле удара равна нулю. Удар заканчивается первой фазой (фазой деформации). Удар называется абсолютно неупругим.
2. k = 1, скорость в конце удара по модулю равна скорости в начале удара. Форма шара полностью восст. Удар называется абсолютно упругим.
3. 0 < k < 1, то u < 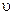 , то есть модуль скорости после удара меньше модуля скорости в начале удар. Удар называется не вполне упругим.
, то есть модуль скорости после удара меньше модуля скорости в начале удар. Удар называется не вполне упругим.
Опытное определение k:
Шарик из испытуемого материала отпускается без нач. скорости с высоты 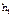 на неподвижную плиту, изготовленную из того же материала. После удара шарик поднимается на высоту
на неподвижную плиту, изготовленную из того же материала. После удара шарик поднимается на высоту 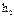 . Скорость шарика в начале удара и в конце удара опр. по ф-ле Галилея:
. Скорость шарика в начале удара и в конце удара опр. по ф-ле Галилея: 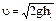 и
и  . Подставим значения скоростей в
. Подставим значения скоростей в 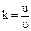 . Получим:
. Получим: 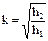 .
.
 2015-05-06
2015-05-06 412
412







