2015-05-06
476
ДИНАМИКА
Задача N93
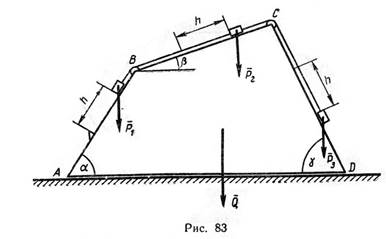Призма ABCD весом Q н лежит на гладкой горизонтальной плоскости. На боковых гранях призмы, образующих с горизонталью углы α, β и γ, расположены три груза, соединенные между собой нерастяжимой нитью, веса которых равны соответственно P 1, P 2 и Р 3 (в ньютонах). В начальный момент система неподвижна.
Определить перемещение призмы относительно неподвижной плоскости, если каждый груз переместится по соответствующей грани на расстояние h м и груз Р 1 опустится при этом вниз (рис. 83, табл. 103).
Таблица 103
| № | ||||||||||
| Q | ||||||||||
| P1 | ||||||||||
| P2 | ||||||||||
| P3 | ||||||||||
| α | 90° | 60° | 45° | 30° | 90° | 60° | 45° | 30° | 90° | 60° |
| β | 30° | 60° | 60° | 30° | 45° | 30° | ||||
| γ | 60° | 45° | 90° | 60° | 45° | 30° | 90° | 45° | 60° | 90° |
| h | 0,4 | 0,4 | 0,5 | 0,5 | 0,6 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 |
Задача N94
Груз М весом Р н, лежащий на краю железнодорожной платформы, передвигается лебедкой А, расположенной на другом конце платформы. Радиус барабана лебедки равен r м. Барабан вращается с постоянным угловым ускорением ε сек -2, причем его начальная угловая скорость равна нулю. Вес платформы вместе с лебёдкой равен Q = 25×104 н. Определить, пренебрегая трением, величину перемещения платформы через t сек после начала передвижения груза (рис. 84, табл. 104).
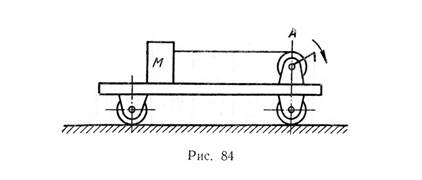
Таблица 104
| № | ||||||||||
| P r | 20000 0,1 | 30000 0,1 | 40000 0,2 | 50000 0,2 | 60000 0,3 | 70000 0,3 | 80000 0,4 | 90000 0.4 | 50 000 0,5 | 0,5 |
| ε | ||||||||||
| t |
