Уравнения Лагранжа второго рода – дифференциальные уравнения второго порядка в обобщенных координатах. Они дают единый и достаточно простой метод решения задач динамики для любых как угодно движущихся голономных и стационарных систем. Число уравнений не зависит от числа входящих в механическую систему точек или тел, а зависит от числа степеней свободы.
Силы, действующие на систему, представлены в виде обобщенных сил, куда входят только внешние силы, а все реакции идеальных связей автоматически исключаются и их можно не показывать на чертеже. Также, если на систему действуют силы трения, то их включают в число внешних сил.
Механическая система под действием силы тяжести приходит в движение из состояния покоя, необходимо определить ускорения всех тел, входящих в систему.
В данном методе решения задачи воспользуемся уравнением Лагранжа второго рода:
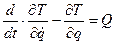 , (1)
, (1)
где: 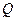 - обобщенные силы;
- обобщенные силы;
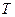 - кинетическая энергия механической системы;
- кинетическая энергия механической системы;
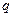 - обобщенная координата;
- обобщенная координата;
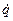 - обобщенная скорость.
- обобщенная скорость.
Покажем на механической системе веса тел 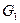 ,
, 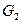 ,
, 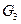 ; обобщённую скорость
; обобщённую скорость 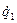 обобщённую координату
обобщённую координату 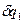 . Схема механической системы указана на рисунке 10.
. Схема механической системы указана на рисунке 10.
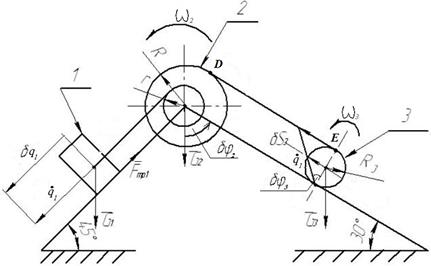
Рис.10
Запишем уравнения взаимосвязи между параметрами:
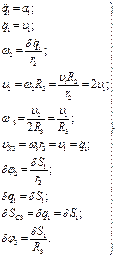 (2)
(2)
где: 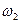 ,
, 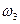 - угловые скорости тел;
- угловые скорости тел;
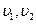 - линейные скорости точек тел;
- линейные скорости точек тел;
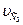 - скорость центра масс однородного катка 3;
- скорость центра масс однородного катка 3;
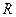 ,
, 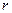 ,
, 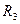 - радиусы тел 2 и 3.
- радиусы тел 2 и 3.
Кинетическая энергия рассматриваемой системы T в конечном ее положении равна сумме кинетических энергий тел 1, 2, 3:
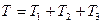 . (3)
. (3)
Кинетическая энергия груза 1, который движется поступательно:
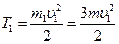 . (5)
. (5)
Кинетическая энергия блока 2, с заданным радиусом инерции, совершающего вращательное движение:
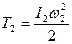 ; (6)
; (6)
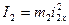 . (7)
. (7)
Используя уравнение (2), получаем:
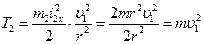 . (8)
. (8)
Кинетическая энергия сплошного однородного цилиндра 3, совершающего плоское движение, складывается из кинетической энергии поступательного движения 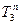 центра тяжести катка и кинетической энергии его вращательного движения
центра тяжести катка и кинетической энергии его вращательного движения 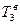 :
:
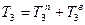 . (9)
. (9)
Определим кинетическую энергию поступательного движения цилиндра 3, используя уравнение связи:
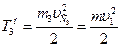 . (10)
. (10)
Определим энергию вращательного движения цилиндра 3, используя уравнение связи:
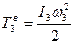 . (11)
. (11)
Момент инерции для сплошного однородного цилиндра 3 равен:
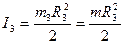 ; (12)
; (12)
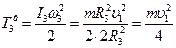 . (13)
. (13)
Тогда кинетическая энергия механической системы будет равна:
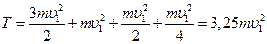 (14)
(14)
Или кинетическая энергия механической системы в обобщенных координатах:
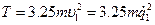 , (15)
, (15)
Дифференцируя выражение (15) по обобщенной координате q1, 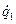 и времени t получим:
и времени t получим:
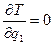 ;
;
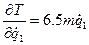 ;
;
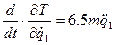 .
.
Обобщенная сила 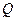 равна отношению алгебраической сумме элементарных работ всех внешних сил, действующих на систему
равна отношению алгебраической сумме элементарных работ всех внешних сил, действующих на систему 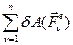 к обобщенной координате
к обобщенной координате 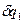 :
:
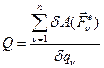 ; (17)
; (17)
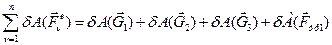 ; (18)
; (18)
Работа груза 1 равна:
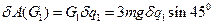 . (19)
. (19)
Работа веса блока 2 будет равна нулю, так как блок 2 не совершает никаких перемещений:
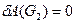 .
.
Учитывая уравнения связи, получаем, что работа веса однородного цилиндра 3 равна:
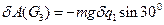 (20)
(20)
Работа силы трения груза 1 равна: (21)
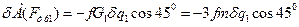 . (22)
. (22)
Сумма элементарных работ механической системы равна:
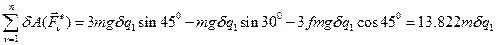 . (23)
. (23)
Подставив (23)в (17),получим значение обобщенной силы 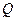 :
:
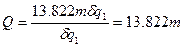 . (24)
. (24)
Подставим (16) и (24) в (1) получим уравнения Лагранжа второго рода в виде:
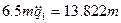 .
.
Из уравнения выразим обобщенное ускорение груза 1:
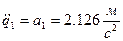 ;
;
Для нахождения ускорений остальных тел подставим значение 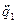 в уравнения взаимосвязи между параметрами:
в уравнения взаимосвязи между параметрами:
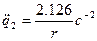 ;
;
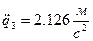 ;
; 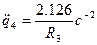 .
.
 2015-05-06
2015-05-06 977
977








