2015-05-06
730
Рассмотрим две СО: инерциальную К и систему К ¢, которая движется относительно К с постоянной скоростью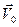 
. Будем считать, что в начальный момент времени t=0 начало координат системы К (т. О) находится на удалении 
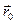от начала координат О системы К. Тогда радиус-векторы любой частицы массы m в моменты времени t и t ¢ в системах К и К¢ связаны соотношениями
.
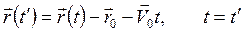• Последнее преобразование ниоткуда не следует, а вводится как постулат классической механики: время абсолютно, т.е. не зависит от состояния движения и течет одинаково во всех СО. Пространство в классической механике также абсолютно.
Преобразования Галилея в координатной форме:
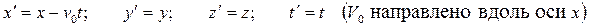
после дифференцирования по времени получим классическую формулу сложения скоростей:
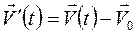
или, как она была записана в кинематике:
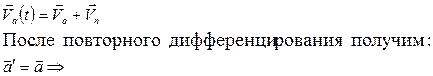
• Все ИСО движутся друг относительно друга с постоянными скоростями.
