Главный вектор и главный момент сил инерции твёрдого тела

Система сил инерции твёрдого тела можно заменить одной силой, равной 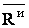и приложенной в центре О, и парой с моментом, равным 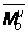. Главный вектор системы сил, как известно, не зависит от центра приведения и может быть вычислен заранее. Т.к. 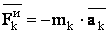, то

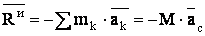(2)

Следовательно, главный вектор сил инерции тела, совершающего любое движение, равен произведению массы тела на ускорение его центра масс и направлен противоположно этому ускорению.

Если ускорение 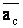разложить на касательное и нормальное, то вектор 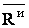разложиться на составляющие

, .

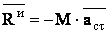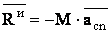Главный момент сил инерции найдём для некоторых частных случаев:

1. Поступательное движение. В этом случае тело никакого вращения вокруг центра масс С не имеет. Отсюда заключаем, что 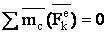, и равенство (1) даёт .

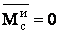Следовательно, при поступательном движении силы инерции твёрдого тела приводят к одной равнодействующей, равной 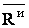и проходящей через центр масс тела.

2. Плоскопараллельное движение. Пусть тело имеет плоскость симметрии и движется параллельно ей. Вследствие симметрии главный вектор и результирующая пара сил инерции, так же как и центр масс С тела, лежат в плоскости симметрии.

Тогда, помещая центр приведения в точке С, получим из равенства (1) 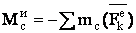. С другой стороны 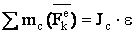. Отсюда заключаем, что

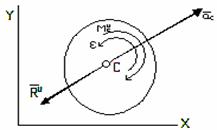
Рис.32

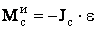(3)

Таким образом, в рассмотренном случае движение системы сил инерции приводится к результирующей силе, равной 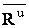[формула (2)] и приложенной в центре масс С тела (рис.32), и к лежащей в плоскости симметрии тела паре, момент которой определяется формулой (3). Знак минус в формуле показывает, что направление момента 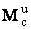противоположно направлению углового ускорения тела.

3. Вращение вокруг оси, проходящей через центр масс тела. Пусть опять тело имеет плоскость симметрии, а ось вращения СZ перпендикулярна к этой плоскости и проходит через центр масс тела. Тогда данный случай будет частным случаем предыдущего. Но при этом 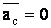, а следовательно, и .

Таким образом, в рассмотренном случае система сил инерции приводится к данной паре, лежащей в плоскости, перпендикулярной к оси вращения тела, и имеющей момент

.

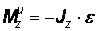При решение задач по формулам (1) и (3) вычисляются модули соответствующих величин, а направление их указывают на чертеже.