Принцип возможных перемещений

Введем понятие о так называемой возможной (или виртуальной) работе, т. е. об элементарной работе, которую действующая на материальную точку сила могла бы совершитьна перемещении, совпадающем с возможным перемещением этой точки. При этом, возможную работу активной силы 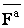будем обозначать символом dА^а

(dА^а=F^а dscosa, где a – угол между направлениями силы и перемещения), а возможную, работу реакции связи 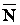- символом dА^r.

Ранее было введено важное понятие о системах с идеальными связями: наложенные на систему связи являются идеальными, если сумма элементарных. работ реакций этих связей при любом возможном перемещении системы равна нулю, т. е.

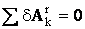. (1)

Рассмотрим систему материальных точек, которая под действием всех приложенных к ней сил и наложенных на нее связей находится в равновесии. Будем при этом все связи системы считать идеальными.

Выделим произвольную точку В_kсистемы и обозначим равнодействующую всех приложенных к ней активных сил (внешних и внутренних) через 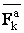, а равнодействующую всех реакций связей (тоже внешних и внутренних) – через 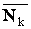. Так как точка В_k вместе со всей системой находится в равновесии, 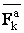+ 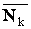=О или 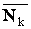= - 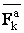. Следовательно, при любом возможном перемещении точки В_k возможные работы dА_k^аи dА^r_k приложенных к ней сил 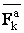и 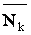будут равны по модулю и противоположны по знаку и в сумме дадут нуль, т. е.

dА_k^а +dА^r_k =0.

Повторяя аналогичные рассуждения, мы получим такие равенства для всех точек системы. Складывая эти равенства почленно, будем иметь:

.

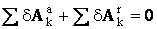Но если наложенные на систему связи являются идеальными, то вторая сумма согласно равенству (1) будет равна нулю. Следовательно, и

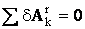(2)

или

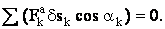
Таким образом, мы доказали, что если механическая система с идеальными связями находится в равновесии, то действующие на нее активные силы удовлетворяют условию (2) Справедлив также и обратный вывод, т. е. если приложенные к механической системе активные силы удовлетворяют условию (2), то система находится в равновесии. Отсюда вытекает следующий принцип возможных перемещений: для равновесия механической системы с идеальными связями необходимо и достаточно, чтобы сумма элементарных работ всех действующих на нее активных сил при любом возможном перемещении системы была равна нулю. Математически необходимое и достаточное условие равновесия любой механической системы выражается равенством (2), которое называют ещё уравнением возможных работ.