Моментом количества движения точки относительно т. О, называется вектор 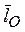 , равный векторному произведению радиус-вектора, проведенного
, равный векторному произведению радиус-вектора, проведенного
из т. О в рассматриваемую точку на вектор ее количества движения (рис.13).

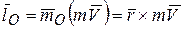 .
.
Понятие момента количества движения точки вводится по аналогии c понятием момента силы:
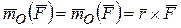 ,
,
т.е. модуль момента количества движения точки можно найти по формуле: 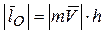 , где h – плечо. Направление вектора
, где h – плечо. Направление вектора 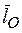 определяется по правилу векторного произведения. Геометрически момент количества движения точки равен удвоенной площади ∆ ОАВ.
определяется по правилу векторного произведения. Геометрически момент количества движения точки равен удвоенной площади ∆ ОАВ.
Теорема: Производная по времени от момента количества движения точки относительно центра О равна сумме моментов сил, действующих на неё, относительно того же центра.
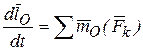 . (27)
. (27)
Доказательство: 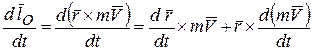 .
.
Но 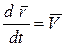 , а по теореме об изменении количества движения
, а по теореме об изменении количества движения 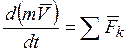 , тогда
, тогда 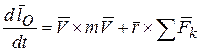 .
.
Учитывая, что векторное произведение двух параллельных векторов равно нулю: 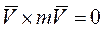 , а
, а 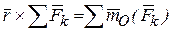 , получим:
, получим:
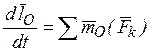 ,
,
что и требовалось доказать.
Теорема об изменении момента количества движения точки векторная, поэтому её можно записать в проекциях на оси координат:
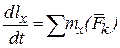 ;
; 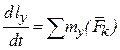 ;
; 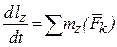 .
.
 2015-05-06
2015-05-06 562
562








