Найдем момент инерции однородного стержня длиной 2 l относительно оси z, проходящей через его центр масс (рис. 21).
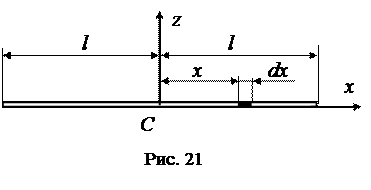
Пусть γ – линейная плотность стержня (масса единицы его длины, кг/м). Выделим на расстоянии х от оси С z элементарный отрезок длиной dx. Момент инерции этого элементарного отрезка относительно оси
С z: 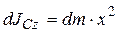 .
.
Но 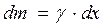 , тогда
, тогда 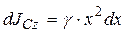 . Проинтегрировав это выражение, получаем
. Проинтегрировав это выражение, получаем
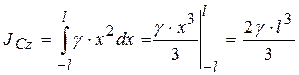 .
.
Но γ ∙2l = m – масса стержня.
Окончательно момент инерции однородного стержня длиной 2 l относительно центральной оси
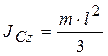 .
.
 2015-05-06
2015-05-06 736
736








