Определение: кинетической энергией точки называется скалярная величина, равная половине произведения массы точки на квадрат ее скорости: 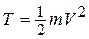 . Пусть точка М перемещается из положения М0 в положение М1 (рис. 19) под действием системы сил
. Пусть точка М перемещается из положения М0 в положение М1 (рис. 19) под действием системы сил  .
.

Воспользуемся основным уравнением динамики в проекции на касательную:  , или
, или
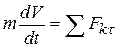 .
.
Учитывая, что 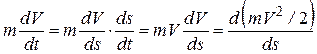 , получим
, получим
 , или
, или
 . (29)
. (29)
Но 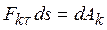 - элементарная работа силы Fk, а
- элементарная работа силы Fk, а 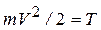 - кинетическая энергия точки. С учетом этого формула (29) примет вид:
- кинетическая энергия точки. С учетом этого формула (29) примет вид:
 или, разделив на dt
или, разделив на dt
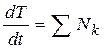 . (30)
. (30)
Формула (30), это и есть теорема об изменении кинетической энергии точки в дифференциальной форме: производная по времени от кинетической энергии точки равна сумме мощностей сил, действующих на нее.
Проинтегрировав выражение (29) в пределах перемещения точки, получим теорему об изменении кинетической энергии в интегральной форме:
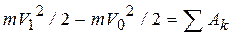 . (31)
. (31)
 2015-05-06
2015-05-06 778
778








