Политропный процесс

Изотермический процесс предполагает идеальный теплообмен с окружающей средой, температура которой в любом процессе принимается неизменной. В адиабатном процессе теплообмен со средой полностью отсутствует. В действительности оба этих предельных случая не могут быть полностью осуществлены. В связи с этим вводят более общий, так называемый политропный процесс, используя для этой цели уравнение

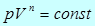(34)

где 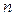- постоянная величина, называемая постоянной политропы; она может принимать значения от 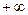до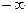

Получим уравнение (34). Напишем первый закон термодинамики в двух видах

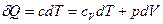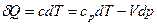и (35)

Из этой системы следует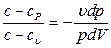

Обозначив 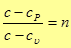(36)

имеем 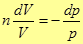(37)

Интегрируя это соотношение при 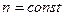, получим

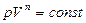(38)

Это выражение называется уравнением политропного процесса.

Учитывая, что 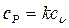, из (36) можно получить формулу теплоемкости 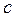в политропном процессе

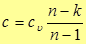(39)

На рис. 2 приведен график функции 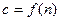(выражение 39)

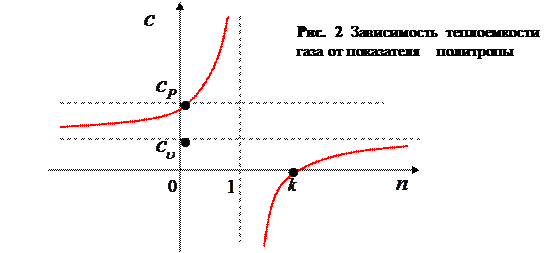
В зависимости от величины 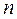политропный процесс может быть, в частности, изотермическим, изобарным, изохорным, адиабатным

1) при 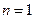уравнение (50) превращается в уравнением изотермического процесса

2) при 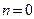из (50) получаем уравнение изобарного процесса

3) при 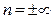уравнение (50) можно записать в виде 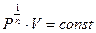из которого следует 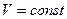, т.е. получили изохорный процесс.

4) при 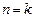выражение (50) переходит в уравнение адиабатного процесса.

1) при 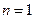(изотермический процесс) теплоемкость стремится к бесконечности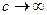

2) при 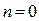(изобарный процесс)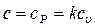

3) при 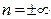(изохорный процесс)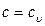

4) при 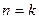(адиабатный процесс)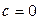

Приведем формулы связи между параметрами состояния идеального газа в политропном

процессе

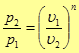
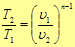
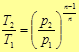(40)