Для иллюстрации процедуры расчета вантовых систем методом сил рассмотрим пример, заимствованный из работы [6].
К расчету принята симметричная однопролетная распорная вантовая система с балкой жесткости, нагруженная сплошной равномерно распределенной по всему пролету нагрузкой 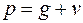 (рис. 4.2, а).
(рис. 4.2, а).
Согласно выражению (4.1) система 6 раз статически неопределима.
В качестве лишних неизвестных принимаются усилия в шести вантах
(рис. 4.2, б). В силу симметрии системы и нагрузки считается, что симметрично расположенные ванты имеют одинаковые усилия. Опорные части на обоих концах балки принимают подвижными. При симметричной нагрузке положение балки изменяться не будет.
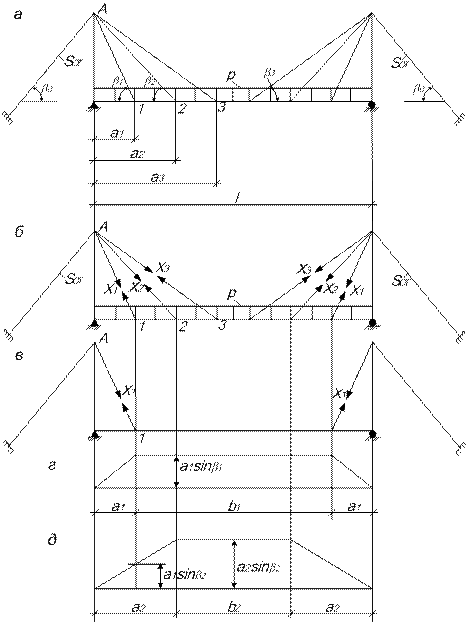
Рис. 4.2. К расчету вантовой системы: а – расчетная схема;
б – основная система; в – схема загружения балки силой Х 1;
г – эпюра изгибающих моментов при действии силы Х1; д – то же силы Х 2
Неизвестные усилия в вантах определятся из системы канонических уравнений вида:
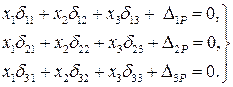 (4.3)
(4.3)
Величины коэффициентов при неизвестных, например 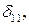 определяют по формуле
определяют по формуле

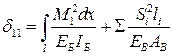 . (4.4)
. (4.4)
На практике установлено, что первое слагаемое значительно больше второго, поэтому можно принять

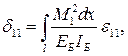 (4.5)
(4.5)
где 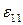 – коэффициент, несколько больший единицы.
– коэффициент, несколько больший единицы.
При  по длине балки интеграл
по длине балки интеграл 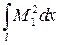 находят, используя рис. 4.2, в, на котором показаны эпюры изгибающих моментов. Умножив эпюру саму на себя, получим
находят, используя рис. 4.2, в, на котором показаны эпюры изгибающих моментов. Умножив эпюру саму на себя, получим
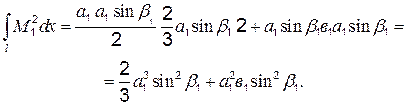
Следовательно,
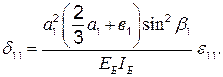 (4.6)
(4.6)
По аналогии с формулой (4.5) коэффициент 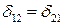
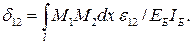 (4.7)
(4.7)
Интеграл 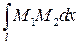 находят перемножением эпюр (рис. 4.2, г, д):
находят перемножением эпюр (рис. 4.2, г, д):
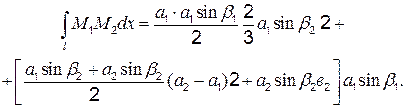
Учитывая, что 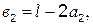 получим
получим
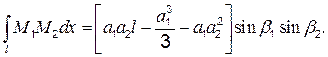
Следовательно,
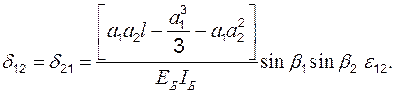 (4.8)
(4.8)
Аналогично можно определить остальные коэффициенты уравнений (4.3):
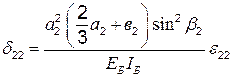 ;
; 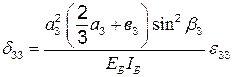 ;
;
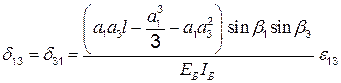 ; (4.9)
; (4.9)
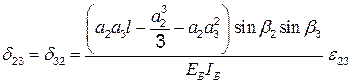 .
.
Для составления системы уравнений (4.3) необходимо определить также грузовые члены. Например,  можно найти как изменение расстояния между концами разрезанного стержня А-1 под действием заданной нагрузки. Для этого сначала находят по формуле строительной механики перемещение узла 1 (см. рис. 4.2) от изгиба балки распределенной нагрузкой p:
можно найти как изменение расстояния между концами разрезанного стержня А-1 под действием заданной нагрузки. Для этого сначала находят по формуле строительной механики перемещение узла 1 (см. рис. 4.2) от изгиба балки распределенной нагрузкой p:
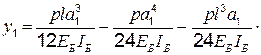
Составляющая перемещения по направлению ванты А-1 будет равна 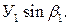 При таких перемещениях работают одновременно две ванты:
При таких перемещениях работают одновременно две ванты:
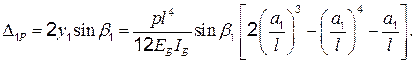 (4.10)
(4.10)
Аналогично можно получить
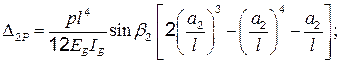 (4.11)
(4.11)
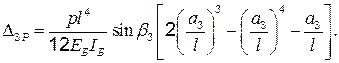 (4.12)
(4.12)
Величины коэффициентов 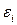 в выражениях (4.6), (4.8), (4.9) можно принять равными:
в выражениях (4.6), (4.8), (4.9) можно принять равными:
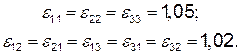
Полученные коэффициенты 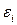 можно, по-видимому, применять в приближенных расчетах вантовых систем с другим числом панелей (от 3 до 9).
можно, по-видимому, применять в приближенных расчетах вантовых систем с другим числом панелей (от 3 до 9).
С учетом полученных значений 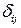 и
и 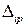 решается система уравнений (4.3), в результате чего находятся неизвестные
решается система уравнений (4.3), в результате чего находятся неизвестные 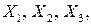 т. е. усилия в вантах соответственно
т. е. усилия в вантах соответственно 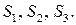 Усилие в оттяжке будет равно:
Усилие в оттяжке будет равно:

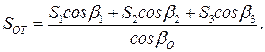 (4.13)
(4.13)
Для определения изгибающих моментов в балке жесткости рассматривается двухопорная балка пролетом 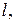 загруженная равномерно распределенной нагрузкой
загруженная равномерно распределенной нагрузкой 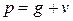 (постоянная g плюс временная
(постоянная g плюс временная 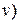 и вертикальными составляющими усилий в вантах (рис. 4.3, а):
и вертикальными составляющими усилий в вантах (рис. 4.3, а):
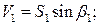
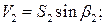
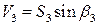 .
.
Для рассматриваемого загружения имеем:
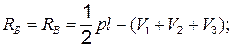
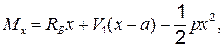 при а <
при а <  < 2 а;
< 2 а;
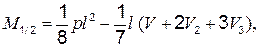 при
при 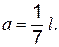
Характер эпюры изгибающих моментов в балке при одинаковых панелях 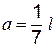 показан на рис. 4.3. Наибольший момент – в середине пролета.
показан на рис. 4.3. Наибольший момент – в середине пролета.
При определении усилий в элементах распорной вантовой системы от изменения температуры используются канонические уравнения вида:
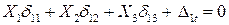 ;
;
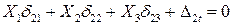 ; (4.14)
; (4.14)
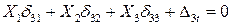 .
.
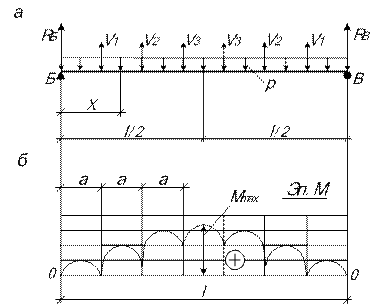
Рис. 4.3. К определению изгибающих моментов в балке жесткости: а – схема загружения балки; б – эпюра изгибающих моментов
Коэффициенты при неизвестных здесь те же, что и в уравнениях (4.3), т. е. определяются по формулам (4.6), (4.8), (4.9). Свободные члены уравнений имеют выражения:
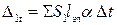 ;
; 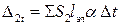 ;
; 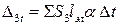 ,
,
где a – коэффициент линейной деформации элемента; 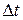 – повышение температуры, °С.
– повышение температуры, °С.
Пользуясь приведенной системой уравнений, можно получить усилия в вантах и их вертикальные составляющие для определения изгибающих моментов в балке жесткости.
Расчеты показывают [6], что изменение температуры существенно влияет на величину изгибающих моментов в балке (25…40 %) и незначительно на усилия в вантах (2…4 %). Не производя решения системы (4.14), можно принимать изгибающий момент в середине пролета балки от изменения температуры:
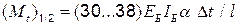 . (4.15)
. (4.15)
Приведенные выше оценки изгибающих моментов в балке даны без учета искусственного регулирования усилий, которое может существенно изменить эти моменты.
Так, с помощью регулирования усилий можно уменьшить изгибающие моменты в балке примерно в два раза при незначительном увеличении усилий в вантах (на 5…10 %). Следовательно, такое регулирование производить целесообразно.
4.2. Приближенные способы расчета
Как видно из подразд. 4.1, расчет вантовых систем громоздок и трудоемок. Поэтому на стадии подготовки исходной информации по характеристикам жесткости элементов 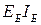 ,
, 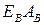 для расчетов точными методами в рамках эскизного проектирования используются приближенные способы определения усилий.
для расчетов точными методами в рамках эскизного проектирования используются приближенные способы определения усилий.
Определение усилий в вантах ведется с помощью упрощенных линий влияния и приближенных выражений в зависимости от пролетности и разновидностей вантово-балочных систем.
Однопролетные распорные вантовые системы. В лучевой вантовой системе (рис. 4.4) ванты работают только при нахождении груза Р = 1 на двух прилегающих панелях. С помощью вырезания узла i получаем для усилия 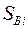 при положении Р = 1 в узле i следующее выражение:
при положении Р = 1 в узле i следующее выражение:
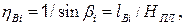
где 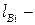 длина i- й ванты;
длина i- й ванты; 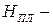 высота пилона.
высота пилона.
Площадь линии влияния 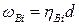 . Тогда усилие
. Тогда усилие 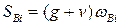 , где
, где 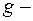 расчетная постоянная нагрузка;
расчетная постоянная нагрузка; 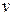 – расчетная временная нагрузка. Для самых длинных вант полученные усилия увеличивают на 30…50 %.
– расчетная временная нагрузка. Для самых длинных вант полученные усилия увеличивают на 30…50 %.
Усилия в оттяжках будут равны
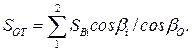
Распор Н будет иметь линию влияния (рис. 4.4) с наибольшей ординатой под узлом 2, имеющей 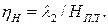 Площадь линии влияния распора
Площадь линии влияния распора 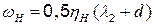 . Тогда величина распора в пилоне
. Тогда величина распора в пилоне 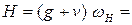
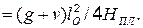 В соответствии с эпюрой продольной сжимающей силы в балке имеем
В соответствии с эпюрой продольной сжимающей силы в балке имеем 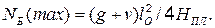
Наибольший изгибающий момент возникает в середине балки жесткости при загружении временной нагрузкой всего пролета и может быть принят равным [6] 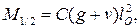 где С = 0,006 – для семипанельной системы, С = 0,007 – для пятипанельной системы.
где С = 0,006 – для семипанельной системы, С = 0,007 – для пятипанельной системы.
Продольные усилия в пилонах принимаются равными
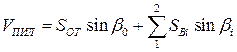 .
.
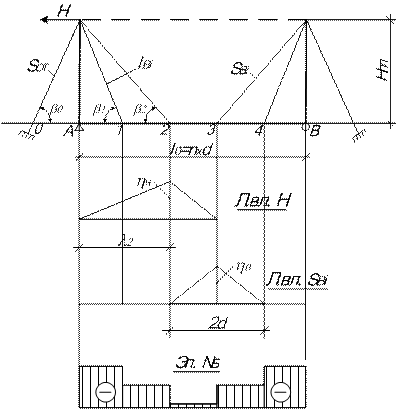
Рис. 4.4. К определению усилий в вантовой однопролетной системе приближенными способами
Двухпролетные безраспорные вантовые системы. В двухпролетных симметричных вантовых системах типа «пучок», «арфа», «веер» (рис. 4.5) с пролетами 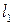 используют линии влияния вертикальных составляющих
используют линии влияния вертикальных составляющих 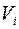 усилий в вантах. Тогда
усилий в вантах. Тогда 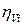 = 1,
= 1, 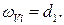
Усилия в вантах 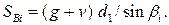 Наибольшее продольное сжимающее усилие в балке возникает в ближайших к пилону панелях и равно
Наибольшее продольное сжимающее усилие в балке возникает в ближайших к пилону панелях и равно 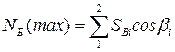 (рис. 4.5), исключая опорную ванту.
(рис. 4.5), исключая опорную ванту.
При неразрезной балке жесткости наибольший изгибающий момент возникает в средней части бокового пролета 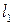
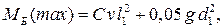 (4.16)
(4.16)
где коэффициент С = 0,007 для многовантовой схемы, С = 0,0085 при количестве панелей в пролете 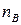 = 9…11.
= 9…11.
Трехпролетные безраспорные вантовые системы (рис. 4.6).
В этих системах (лучевой, радиально-лучевой, веерной, «арфа») усилия в вантах определяются по формуле проф. В.К. Качурина:
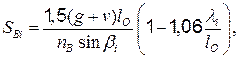 (4.17)
(4.17)
где g – расчетная постоянная нагрузка; 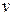 – то же временная при загружении ею основного пролета;
– то же временная при загружении ею основного пролета; 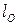 – длина основного пролета;
– длина основного пролета; 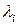 – расстояние от пилона до точки прикрепления соответствующей ванты;
– расстояние от пилона до точки прикрепления соответствующей ванты; 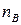 – число вант, поддерживающих балку в основном пролете;
– число вант, поддерживающих балку в основном пролете; 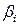 – угол наклона к оси балки рассматриваемой ванты.
– угол наклона к оси балки рассматриваемой ванты.
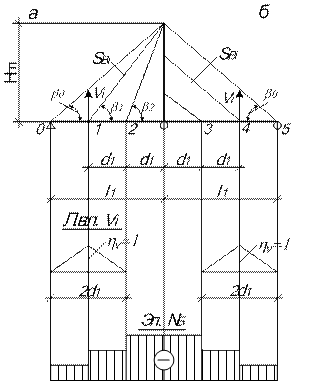
Рис. 4.5. К определению усилий в вантовой двухпролетной системе приближенным способом
Усилия в вантах боковых пролетов, кроме оттяжек, можно принимать такими же, как и в симметричных им вантах основного пролета. Усилие в оттяжке определяют из условия передачи на нее горизонтальных составляющих усилий всех вант основного пролета, жестко связанных с ней на пилоне (рис. 4.6). Тогда
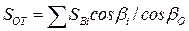 .
.
Продольные усилия в балке определяют исходя из полученных усилий в вантах. Наибольшее продольное сжимающее усилие в балке (рис. 4.6, в) возникает в примыкающих к пилонам панелях и составляет
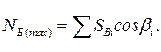
Наибольший изгибающий момент в балке жесткости определяется по формуле
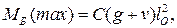 (4.18)
(4.18)
где С – коэффициент, принимаемый равным: 0,007 – при пяти-, 0,006 – при девяти- и 0,005 – при многовантовых системах.
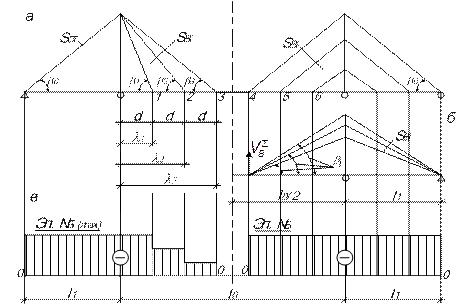
Рис. 4.6. К определению усилий в вантовой трехпролетной системе приближенным способом
В системе «звезда» (рис. 4.6, б) усилия в отдельных вантах определяются из условия 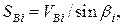 где
где 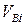 – вертикальная составляющая усилия в отдельной ванте, определяется как
– вертикальная составляющая усилия в отдельной ванте, определяется как
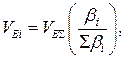 а величина
а величина 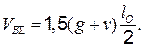
Кроме расчета на постоянную и временную нагрузки, вантовые системы рассчитывают на влияние изменения температуры с учетом коэффициентов сочетания этих нагрузок. В предварительных расчетах внешне безраспорных вантовых систем с балками жесткости этим влиянием можно пренебречь. Продольное усилие в балке 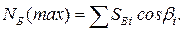
4.3. Определение деформаций (прогибов) вантовых систем
Наибольшие прогибы в одно- и трехпролетных вантовых системах происходят в середине пролета при загружении временной нагрузкой всего основного пролета, так как при этом возникают максимальные напряжения в крайних вантах и оттяжках и происходит их наибольшее удлинение.
При этом пренебрегаем влиянием жесткости балки и ее продольными деформациями, т. е. балка жесткости рассматривается как шарнирная цепь из абсолютно жестких звеньев.
Рассмотрим однопролетную лучевую вантовую систему и определим вертикальное перемещение точки  в средней части пролета (рис. 4.7, а).
в средней части пролета (рис. 4.7, а).
Рис. 4.7. К определению деформаций вантовой системы: а – схема системы; б – схема деформирования системы
При загружении всего пролета временной нагрузкой напряжения 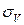 в крайней ванте
в крайней ванте 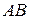 и оттяжке
и оттяжке 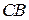 принимаются одинаковыми
принимаются одинаковыми
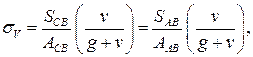
где 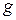 и
и 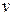 – соответственно расчетные интенсивности от постоянных и временных нагрузок;
– соответственно расчетные интенсивности от постоянных и временных нагрузок; 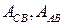 – площади сечения вант.
– площади сечения вант.
На основании построения кинематической схемы формирования вертикальной деформации системы в точке А (рис. 4.7, б) получим:
- удлинение оттяжки
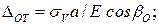
- горизонтальное перемещение вершины пилона и точки 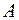 в мнимое положение
в мнимое положение 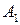
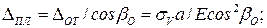
- вертикальное перемещение точки 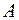 вследствие реализации перемещения по линии
вследствие реализации перемещения по линии 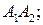 тогда
тогда
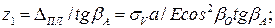
- удлинение ванты 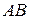 на величину
на величину
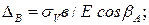
- дополнительное вертикальное перемещение точки 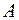 вследствие удлинения ванты
вследствие удлинения ванты 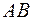
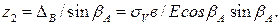
Сложив 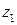 и
и 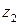 , получим полное перемещение точки, т. е. прогиб балки жесткости под действием временной нагрузки:
, получим полное перемещение точки, т. е. прогиб балки жесткости под действием временной нагрузки:
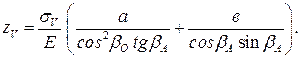 (4.19)
(4.19)
Если считать величину 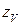 равной нормированному значению прогиба пролетного строения [ z ], принимаемого в зависимости от назначения моста [10], можно установить граничный уровень напряжений в вантах от одной временной нормативной нагрузки
равной нормированному значению прогиба пролетного строения [ z ], принимаемого в зависимости от назначения моста [10], можно установить граничный уровень напряжений в вантах от одной временной нормативной нагрузки
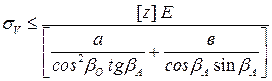 .
.
Следовательно, чтобы прогиб от временной нагрузки 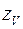 не превосходил нормируемой величины [ z ], напряжение от полной нагрузки
не превосходил нормируемой величины [ z ], напряжение от полной нагрузки 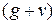 не должно превышать следующего значения
не должно превышать следующего значения
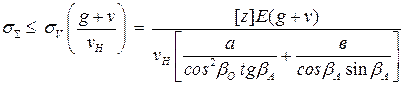 . (4.20)
. (4.20)
Для определения приближенных значений прогибов вантовых систем с целью контролирования и обеспечения их жесткости 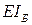 можно использовать условие
можно использовать условие
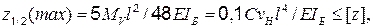 (4.21)
(4.21)
где 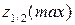 – наибольшие прогибы, характерные для середины пролета одно-, двух- и трехпролетных систем при загружении нормативной временной нагрузкой
– наибольшие прогибы, характерные для середины пролета одно-, двух- и трехпролетных систем при загружении нормативной временной нагрузкой 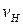 одного пролета
одного пролета 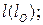 С – коэффициент, принимаемый в зависимости от пролетности вантово-балочных систем (подразд. 4.2); [ z ] – нормируемый прогиб [10].
С – коэффициент, принимаемый в зависимости от пролетности вантово-балочных систем (подразд. 4.2); [ z ] – нормируемый прогиб [10].
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Дайте общую характеристику аналитических методов расчета ВМ.
2. Приведите основные положения применения метода сил в расчетах ВМ.
3. Рассмотрите приближенные способы определения усилий в элементах ВМ.
4. Как определяются деформации (прогибы) вантовых систем?
5. ПРАКТИЧЕСКИЙ РАСЧЕТ НЕСУЩИХ ЭЛЕМЕНТОВ
ВИСЯЧИХ И ВАНТОВЫХ МОСТОВ
5.1. Общие замечания
Статический расчет висячих и вантовых мостов можно подразделить на два этапа:
1) определение внутренних усилий 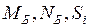 и перемещений
и перемещений 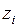 от комбинаций нагрузок (постоянной, временной, температурной) при помощи изложенных выше аналитических методов;
от комбинаций нагрузок (постоянной, временной, температурной) при помощи изложенных выше аналитических методов;
2) уточнение размеров поперечных сечений несущих элементов (кабеля, подвесок, вант, балки жесткости, пилонов) на основе проверок по прочности, выносливости и жесткости.
При определении усилий для расчета элементов пролетных строений на прочность рассматриваются два вида сочетаний нагрузок:
– основное, куда включаются: нагрузка от собственного веса конструкций; воздействие регулирования усилий; вертикальная нагрузка от подвижного состава, пешеходов и различных транспортируемых технических средств. Указанные нагрузки учитываются с коэффициентами сочетаний 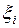 = 1,0;
= 1,0;
– особое, куда включаются нагрузки основного сочетания, а также температурные климатические воздействия. Нагрузки особого сочетания учитываются со следующими значениями коэффициентов сочетания: для постоянных нагрузок и транспортируемых технических средств 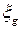 = 1,0; для временной нагрузки от подвижного состава и пешеходов
= 1,0; для временной нагрузки от подвижного состава и пешеходов 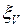 = 0,8; для температурных воздействий
= 0,8; для температурных воздействий 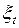 = 0,7.
= 0,7.
Расчеты элементов на выносливость производятся на основное сочетание нагрузок.
Расчеты висячих и вантовых систем по жесткости (деформациям) выполняются дважды:
– на воздействие только временной вертикальной нагрузки n при 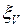 = 1,0;
= 1,0;
– на воздействие временной вертикальной нагрузки и температурное воздействие при 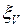 = 0,8;
= 0,8; 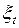 = 0,7.
= 0,7.
Величины нагрузок и воздействий для расчета элементов пролетных строений висячих и вантовых мостов по всем группам предельных состояний принимаются с коэффициентами надежности по нагрузке 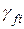 и динамическим коэффициентом
и динамическим коэффициентом 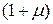 согласно табл. 5.1 [10].
согласно табл. 5.1 [10].
Значения коэффициентов надежности к нагрузкам 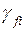 принимаются:
принимаются:
– для постоянных нагрузок по [10, п. 2.10];
– для временных нагрузок и воздействий по [10, пп. 2.23, 2.32].
Таблица 5.1
Коэффициенты к нагрузкам
| Вид расчета элементов висячих и вантовых систем | Вводимые коэффициенты | ||
| к постоянным нагрузкам | к подвижной вертикальной нагрузке | к температурному воздействию | |
| Расчет на прочность | 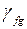 | 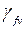 , (1 + m) , (1 + m) | 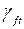 = 1,2 = 1,2 |
| Расчет на выносливость | 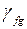 = 1 = 1 | 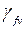 = 1, (1 + 2/3 m) = 1, (1 + 2/3 m) | – |
| Расчеты по жесткости, включая расчет по образованию трещин в железобетонных элементах |  = 1 = 1 |  = 1, (1 + m) = 1 = 1, (1 + m) = 1 |  = 1 = 1 |
Величина динамического коэффициента (1 + m) к вертикальным нагрузкам СК, АК, а также к нагрузкам от поездов метрополитена и трамвая при расчете элементов главных ферм (балок) и пилонов висячих и вантовых моcтов определяется как [10]
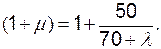
К вертикальным подвижным нагрузкам для пешеходных мостов, к нагрузкам на тротуарах, к техническим нагрузкам трубопроводов
(1 + m) = 1,0.
Нормативная временная вертикальная нагрузка 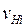 от подвижного состава различного вида и пешеходов принимается в соответствии с требованиями СНиП 2.05.03-84* [10 пп. 2.11–2.15, 2.21].
от подвижного состава различного вида и пешеходов принимается в соответствии с требованиями СНиП 2.05.03-84* [10 пп. 2.11–2.15, 2.21].
 2015-04-20
2015-04-20 822
822








