Пусть дана ф-я 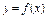 , опред. на
, опред. на 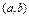 . Выберем любую т.
. Выберем любую т. 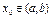 и дадим нек. приращ.
и дадим нек. приращ. 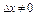 (настолько малое, что
(настолько малое, что 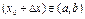 ) Приращ. ф-и в т.
) Приращ. ф-и в т. 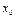 :
: 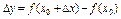
Опр. Производной ф-ей от 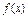 наз. предел отношения приращения ф-и
наз. предел отношения приращения ф-и 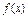 к приращ. ее аргумента, когда последн.
к приращ. ее аргумента, когда последн. 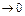
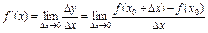
Опр. 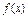 наз. дифференцируемой в т.
наз. дифференцируемой в т. 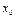 , если
, если 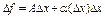
A=const, не зависящ. от 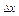 ,
, 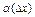 - бмф при
- бмф при 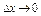
Th. 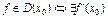
Утв: 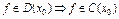 , т. е.
, т. е. 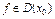 если
если 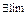 слева =
слева = 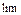 справа
справа
Опр. Лин. часть приращ. ф-и наз. диф-лом ф-и 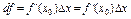
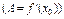
Th. 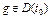 ,
, 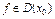 ,
, 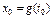 , то
, то 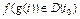 :
: 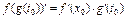
Th. 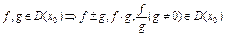
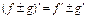
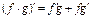
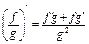
Th. 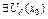 :
: 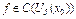 , монот,
, монот, 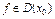 ,
, 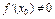 , тогда
, тогда 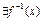 ,
, 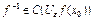 , монот.,
, монот., 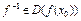
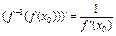 .
.
Опр. 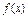 наз. возраст. в т.
наз. возраст. в т. 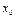 если сущ. нек окр-ть этой т. в кот.
если сущ. нек окр-ть этой т. в кот.
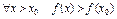
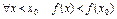 .
.
Опр. 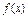 наз. убыв. в т.
наз. убыв. в т. 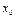 если сущ. нек окр-ть этой т. в кот.
если сущ. нек окр-ть этой т. в кот.
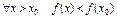
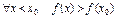 .
.
Замечание: 1 Если ф-я возраст. (убыв.), то она возраст (убыв.) в т. 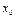 .
.
2 Если ф-я возраст. (убыв.) в т. 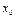 , то она не обяз. возраст (убыв).
, то она не обяз. возраст (убыв).
Th1. 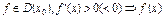 возр. (убыв.) в т.
возр. (убыв.) в т. 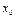
Необх. усл-я экстремума.
Опр. Ф-я имеет в т. 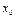 loc max (min), если в нек проколотой окр-ти этой т. вып-ся
loc max (min), если в нек проколотой окр-ти этой т. вып-ся 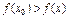 (
(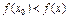 )
)
Опр. Ф-я имеет loc экстремум в т. 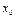 , если в этой т. она имеет или loc min или loc max.
, если в этой т. она имеет или loc min или loc max.
Th (Ферма): 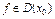 ,
, 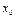 - loc extr.
- loc extr. 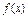
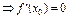 .
.
Док-во: По усл. 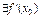
Т.к. 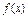 имеет в т.
имеет в т. 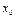 loc extr, то она не может в этой точке ни возр. ни убыв, тогда по th1
loc extr, то она не может в этой точке ни возр. ни убыв, тогда по th1 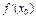 не м. б. >0 или <0,
не м. б. >0 или <0, 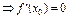 .
.
Th Ролля: 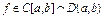 ,
, 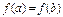
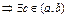 :
: 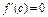
Док-во: 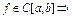 (th Вейерштрасса)
(th Вейерштрасса) 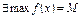 ,
, 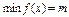
1) 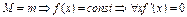
2) 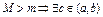 , что
, что 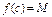 или
или 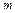 (т.к.
(т.к. 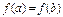 )
) 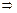 (th Ферма)
(th Ферма) 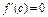
Th Лагранжа: 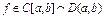
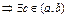 :
: 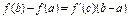 .
.
Док-во: введем 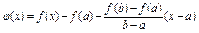
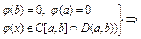 (th Ролля)
(th Ролля) 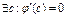
(разность 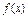 и лин. ф-и)
и лин. ф-и)
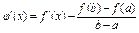
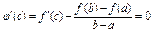
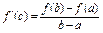
Сл- я:
 2015-04-20
2015-04-20 571
571








