Формула Тейлора диференнційовної функції та її залишковий член. Формула Тейлора для елементарних функцій та її застосування

Предположим, что функция 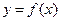имеет все производные до 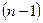-го порядка включительно в некотором промежутке, содержащем точку 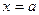, а в этой точке – до 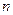-го порядка. Найдем многочлен 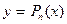степени не выше 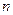, значение которого в точке 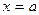равняется значению функции 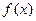в этой точке, а значения его производных до 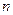-го порядка в точке 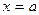равняются значениям соответствующих производных от функции 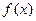в этой точке:

.

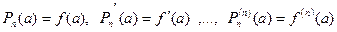Будем искать этот многочлен в форме многочлена по степеням 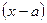с неопределенными коэффициентами: . (*)

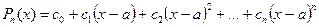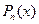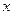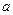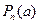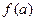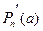Далее находим производные от . Подставляя в левые и правые части этих производных вместо значение и заменяя через , через 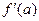и т.д., получим

.

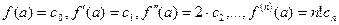Откуда находим неизвестные коэффициенты 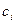, и подставляя их в формулу (*), получим искомый многочлен

.

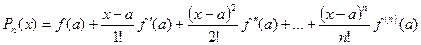Обозначим через 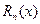разность значений данной функции 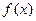и построенного многочлена 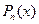: 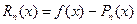, откуда 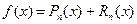, или в развернутом виде

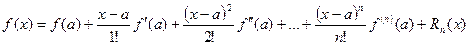
Т. о. мы получили ф-лу Тейлора ф-и одной действ. пер-й. 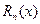наз-ся остаточным членом.