Ряд Тейлора

Пусть ф-я 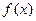имеет производные любого порядка в окрестности точки 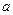. Для такой ф-и можно составить ряд:

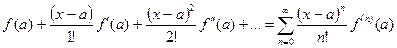Независимо от того, сх-ся или расх-ся этот ряд, он наз. рядом Тейлора ф-и 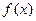по степеням 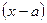. Если 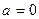, то соответствующий ряд называют рядом Маклорена.

Теорема1. Если ф-я 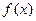имеет на отрезке 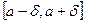производные любого порядка и остаточный член стремится к 0 при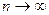

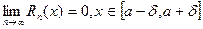
на этом отр., то 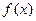раскладывается в сх-ся к ней ряд Тейлора на этом отр.

Теорема2. Если функция 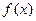имеет на отрезке 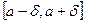производные любого порядка, ограниченные одним и тем же числом 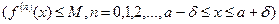, то остаточный член на этом отрезке стремится при 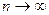к 0.