1. 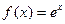 Эта функция бесконечно дифферкнцируема на
Эта функция бесконечно дифферкнцируема на 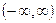 . При этом
. При этом
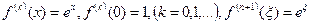 .
.
Формула Тейлора с остаточным членом в форме Лагранжа имеет вид
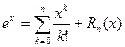 ,
, 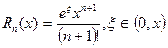 ,
,
где 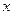 может быть положительным и отрицательным. На отрезке
может быть положительным и отрицательным. На отрезке 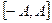 ,
, 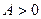
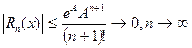 .
.
Это показывает, что функция 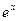 раскладывается на
раскладывается на 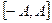 в сходящийся к ней ряд Тейлора по степеням
в сходящийся к ней ряд Тейлора по степеням 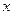 (ряд Маклорена):
(ряд Маклорена):
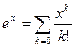 .
.
Но 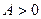 произвольное число, поэтому это равенство имеет место на всей действительной оси.
произвольное число, поэтому это равенство имеет место на всей действительной оси.
2. 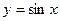 Данная функция имеет производную любого порядка и
Данная функция имеет производную любого порядка и
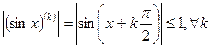 .
.
Поэтому по теореме 2 функция 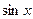 раскладывается в сходящийся к ней на
раскладывается в сходящийся к ней на 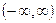 ряд Тейлора по степеням
ряд Тейлора по степеням 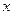 :
:
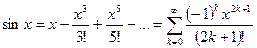 .
.
3. 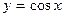 Совершенно аналогично можно получить, что
Совершенно аналогично можно получить, что
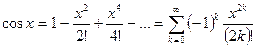 .
.
4. 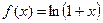 Эта функция определена и сколько угодно раз дифференцируема для
Эта функция определена и сколько угодно раз дифференцируема для 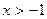 . Поэтому для нее формулу Тейлора можно написать для любого
. Поэтому для нее формулу Тейлора можно написать для любого 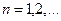 при
при 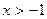 . Так как
. Так как
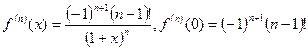 ,
,
то формула Тейлора имеет вид
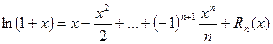 .
.
Используя ф-лы лагранжа и Коши остаточного члена можно показать, что 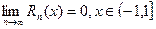 . Поэтому ф-я
. Поэтому ф-я 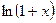 раскладывается в указанном промежутке в ряд Тейлора по степеням
раскладывается в указанном промежутке в ряд Тейлора по степеням 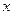 :
:
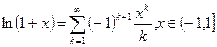 .
.
5. 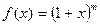 Для этой функции
Для этой функции
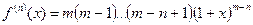 ,
, 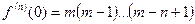 .
.
Формула Тейлора по степеням 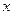 имеет вид
имеет вид
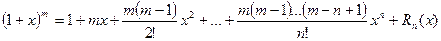 .
.
Можно доказать, что при любом 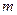 :
: 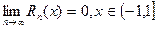 . Поэтому для любого действительного
. Поэтому для любого действительного 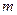 имеет место разложение функции
имеет место разложение функции 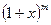 в ряд Тейлора по степеням
в ряд Тейлора по степеням 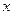 :
:
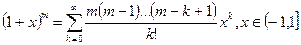 .
.
 2015-04-20
2015-04-20 884
884








