2015-04-20
1130
Мерой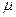 
, заданной на произвольной системе 
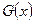подмножеств множества х наз. такая функция 
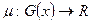, которая удовлетворяет 2-е аксиомы: 1) 
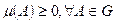- неотрицательность; 2) если А, В 
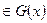и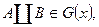 
то справедливо равенство: 
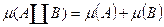- условие адетивности. Мерой Лебега – мера 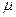заданная на 
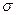- алгебре 
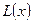соотношением 
.(
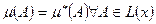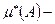внешняя мера множества А). 
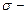алгебра: счетно – адетивная мера 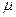задана на полукольце Р(х) подмножеств х, для которых 
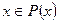; символом 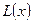будем обозначать совокупность всех таких подмножеств мн-ва х, каждое из которых измеримо по Лебегу, отсюда алгебра 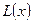является 
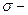алгеброй. Счетно-аддетивная мера- мера 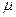заданная на системе G(x) подмн-в мн-ва х, если она удовл-т след. условию: 
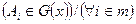и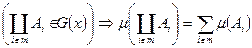 
- условие аддетивности меры.
Множество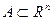 
наз. n-мерным паралелепип-м, если существуют такие промежутки 
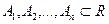, что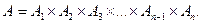 
Для чисел 
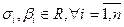удовлетворяющих условию 
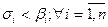. Рассмотрим порождаемое ими множество В задаваемое равенством: 
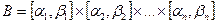. Рассмотрим совокупность Р(В) всех n- мерных параллелепипедов, содержащихся в В. Очевидно, эта система является полукольцом. Зададим на этой системе меру m след. образом: 
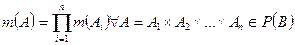, где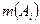 
обозначает длину промежутка 
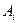. Т.о. мере паралелеп. А= его n-мерному V. Поскольку В 
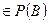, то указанную меру m можно продолжать до счетно-адетивной меры 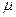, заданной на 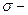алгебре L(B) след. образом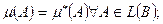 
; 
.
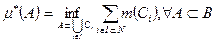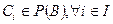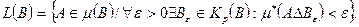Обозначим теперь символом 
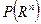совокупность всех n-мерных парал-в содержащихся в 
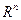. Рассмотрим систему 
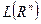и обобщенную меру 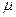, задав их след образом: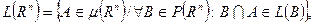 
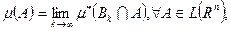
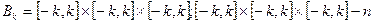раз.
Множество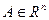 
наз. измеримым по Лебегу, если, и только если 
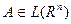. Построенная обобщенная мера 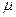наз. мерой Лебега в n-мерном Евклидовом пр-ве.
