Если один из концов отрезка считают начальным, а другой конечным, то на отрезке устанавливают направление от начала к концу, такой отрезок называется направленным или вектором. Если 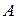 начало, а
начало, а 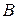 конец, то вектор обозначают
конец, то вектор обозначают 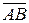 . Модулем вектора
. Модулем вектора 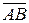 называют его длину и обозначают
называют его длину и обозначают 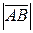 . Вектор наз. нулевым если начало и конец совпадают, т. е. длинна вектора равна 0 Вектор, модуль которого равен единице наз. единичным или ортом.
. Вектор наз. нулевым если начало и конец совпадают, т. е. длинна вектора равна 0 Вектор, модуль которого равен единице наз. единичным или ортом.
Скалярным произведением 2-х не нулевых векторов 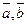 наз. число
наз. число 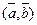 , равное произведению длин перемножаемых векторов на cos угла между ними:
, равное произведению длин перемножаемых векторов на cos угла между ними: 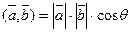 . Если один из векторов
. Если один из векторов 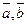 явл. нулевым, то считают, что
явл. нулевым, то считают, что 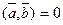 . Свойства:
. Свойства:
1. 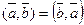 - коммутативность скалярного произведения. Док-во: по определению
- коммутативность скалярного произведения. Док-во: по определению 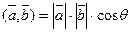 ,
, 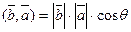 , как видим, если
, как видим, если 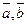 не нулевые векторы, то
не нулевые векторы, то 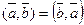 . Если один из векторов нулевой, то
. Если один из векторов нулевой, то 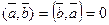 . Таким образом каковы бы не были векторы
. Таким образом каковы бы не были векторы 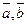
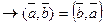 .
.
2. 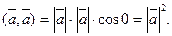
3. Если 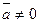 ,то
,то 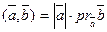 (pr-проекция).
(pr-проекция).
4. 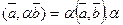 - любое действ. число.
- любое действ. число.
5. 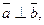 необходимо и достат-но
необходимо и достат-но 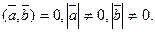
6. 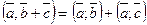 . Угол между векторами: по определению
. Угол между векторами: по определению 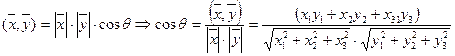 .
.
Векторное произведение 2-х векторов. Если 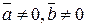 , то векторным произведением векторов
, то векторным произведением векторов 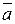 и
и 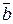 наз. вектор
наз. вектор 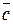 длинна и направление которого определяется следующим образом
длинна и направление которого определяется следующим образом 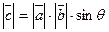 ,
, 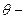 угол между
угол между 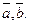 Если
Если 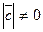 , то
, то 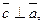
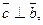 и направлен так чтобы тройка
и направлен так чтобы тройка 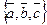 была правой. Для обозначения вект. произведения пользуются такими символами
была правой. Для обозначения вект. произведения пользуются такими символами 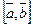 или
или 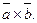 Если
Если 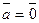 или
или 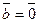 , то считают
, то считают 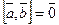 .
.
Св-ва:
1. Если 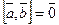 , то
, то 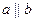 , верно и обратное утверждение. Док-во: Если
, верно и обратное утверждение. Док-во: Если 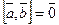 , то возможны такие варианты: а) один из векторов
, то возможны такие варианты: а) один из векторов 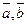 - нулевой. Ясно, что
- нулевой. Ясно, что 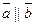 . б)
. б) 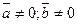 , тогда
, тогда 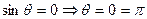 , в обоих случаях
, в обоих случаях 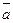 компланарно
компланарно 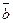 .(компланарны, если они || одной плоскости).
.(компланарны, если они || одной плоскости).
2. 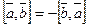 .
.
3. Длина вект. произведения 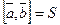 парал. построенного на векторах
парал. построенного на векторах 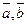 , кот. откладываются из одной точки.
, кот. откладываются из одной точки.
4. Вект. произвед. 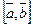 не изменится, если один из сомножителей
не изменится, если один из сомножителей 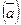 заменить ортогональной проекцией на плоскость
заменить ортогональной проекцией на плоскость 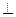 пл-ти b, т. е.
пл-ти b, т. е. 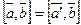 .
.
5. 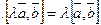 ;
; 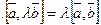 .
.
6. 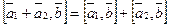 ;
; 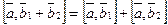 .
.
7. Пусть 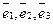 - правый декартовый базис и пусть в этом базисе
- правый декартовый базис и пусть в этом базисе 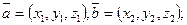
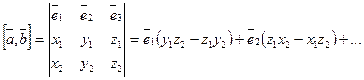
Двойным векторным произв. 3-х векторов наз. вектор 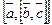 или
или 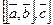 . Теорема.
. Теорема. 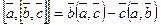
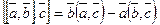
Смешанное произ. 3-х векторов 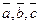 наз. число
наз. число 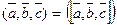 . Теорема (геометр. смысл). Пусть V-обьем паралел. построенного на векторах
. Теорема (геометр. смысл). Пусть V-обьем паралел. построенного на векторах 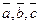 , тогда
, тогда 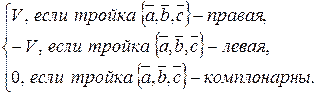
36. ПРЯМАЯ НА ПЛОСОСТИ. УРАВНЕНИЕ ПРЯМОЙ НА ПЛ-ТИ В ПРЯМОУГОЛЬНОЙ ДЕКАРТОВОЙ СИСТЕМЕ КООРДИНАТ.
Построим ур-е прямой, кот. проходит через точку 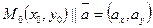 ,
, 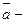 направляющий вектор.
направляющий вектор. 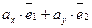 , если
, если 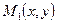 некоторая точка прямой, то тогда и только тогда
некоторая точка прямой, то тогда и только тогда 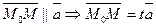 .(
.(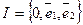 -репер).
-репер). 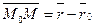 , таким образом для произвольной точки М прямой
, таким образом для произвольной точки М прямой 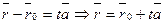 (1). Ур-е (1) наз. векторным уравнением прямой, кот. проходит через точку
(1). Ур-е (1) наз. векторным уравнением прямой, кот. проходит через точку 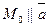 . Очевидно
. Очевидно 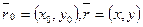 . Из (1) получаем параметрическое уравнение прямой:
. Из (1) получаем параметрическое уравнение прямой: 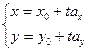 (2). Из парам. уравнения следует каноническое уравнение прямой на плоскости:
(2). Из парам. уравнения следует каноническое уравнение прямой на плоскости: 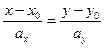 (3). Прямая проходит через точку
(3). Прямая проходит через точку 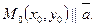 Запишем ур-е прямой кот. проходит через 2-е точки
Запишем ур-е прямой кот. проходит через 2-е точки 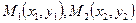 . Воспользуемся каноническим ур-м (3), в качестве направляющего вектора возьмем вектор
. Воспользуемся каноническим ур-м (3), в качестве направляющего вектора возьмем вектор 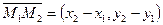 , в итоге получим:
, в итоге получим: 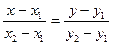 (4). Рассмотрим каноническое ур-е прямой
(4). Рассмотрим каноническое ур-е прямой 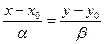 . Из него получаем:
. Из него получаем: 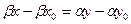 ,
, 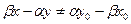 , тогда последнее уравнение можно записать в виде
, тогда последнее уравнение можно записать в виде 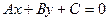 (5)- общее уравнение прямой. Из сказанного выше можно сделать вывод, что направляющий вектор прямой
(5)- общее уравнение прямой. Из сказанного выше можно сделать вывод, что направляющий вектор прямой 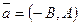 .
.
Теорема.(взаимное расположение на пл-ти) Пусть на плоскости заданы две прямые 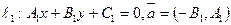 ;
; 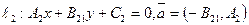 , тогда 1) прямые пересекаются, если
, тогда 1) прямые пересекаются, если 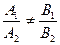 ; 2) прямые ||, если
; 2) прямые ||, если 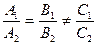 ; 3) прямые совпадают, если
; 3) прямые совпадают, если 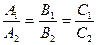 . Совокупность прямых на пл-ти, кот. проходит через одну точку
. Совокупность прямых на пл-ти, кот. проходит через одну точку 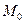 наз. пучком прямых с центром в точке
наз. пучком прямых с центром в точке 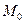 . Нормальный вектор прямой: (
. Нормальный вектор прямой: (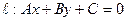 -прямая)-это любой вектор
-прямая)-это любой вектор 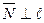 . Лемма1. Для прямой
. Лемма1. Для прямой 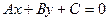 ,
, 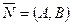 . Лемма2. Угол
. Лемма2. Угол 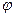 между 2-мя прямыми понимают наименьший угол из 2-х смешанных углов, образованных этими прямыми. Теорема. Пусть
между 2-мя прямыми понимают наименьший угол из 2-х смешанных углов, образованных этими прямыми. Теорема. Пусть 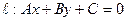 ,и
,и 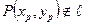 , тогда расстояние от точки Р до прямой можно вычислить по формуле:
, тогда расстояние от точки Р до прямой можно вычислить по формуле: 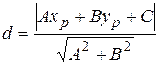 .
.
 2015-04-20
2015-04-20 969
969








